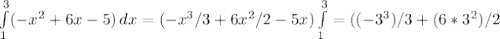-5*3)-((-1)^3/3+(6*1^2)/2-5*1)=3-(-7/3)=16/3
В решении.
Объяснение:
Решите задачу с составления уравнения. Разность двух чисел равна 3, а разность их квадратов 69. Найдите эти числа.
х - первое число.
у - второе число.
По условию задачи система уравнений:
х - у = 3
х² - у² = 69
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 3 + у
(3 + у)² - у² = 69
9 + 6у + у² - у² = 69
6у = 69 - 9
6у = 60
у = 60/6
у = 10 - второе число.
х = 3 + у
х = 3 + 10
х = 13 - первое число.
Проверка:
13 - 10 = 3, верно.
13² - 10² = 169 - 100 = 69, верно.
В решении.
Объяснение:
а)Является ли последовательность бесконечно убывающей геометрической прогрессией если она задана формулой bn=(-4)ⁿ⁺²?
Если знаменатель |q|<1, то такая последовательность называется бесконечно убывающей геометрической прогрессией.
Значит, чтобы ответить на вопрос задания, нужно вычислить q.
b₁ = (-4)¹⁺² = (-4)³ = -64;
b₂ = (-4)²⁺² = (-4)⁴ = 256;
q = b₂/b₁
q = 256/-64
q = -4.
|q| = |-4|
|q| > 1, значит, данная прогрессия не является бесконечно убывающей геометрической прогрессией.
б)Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.
Периодическая дробь — бесконечная десятичная дробь, в которой, начиная с некоторого места, стоит только периодически повторяющаяся определенная группа цифр.
0,(12) = 0,121212121212 до бесконечности.
Чтобы производить какие-то действия с периодической дробью, её нужно округлить до сотых:
0,(12) ≈ 0,12.
0,(12)=4/33.
ответ: