Максимум в точке х =  (для записи
(для записи 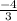 )
)
Минимум в точке х = -1
Объяснение:
f(x)=2x^3+7x^2+8x+4
Область определения:
Х∈R
f(x)=2x^3+7x^2+8x+4, Х∈R
Определим производную f:
f(x) = 2x^3+7x^2+8x+4
f'(x) = d/dx (2x^3+7x^2+8x+4)
f'(x) = d/dx(2x^3) + d/dx(7x^2) + d/dx(8x) + d/dx(4)
f'(x) = 2*3x^2 + 7*2x+8+0
f'(x) = 6x^2+14x+8
f'(x) = 6x^2+14x+8, Х∈R
Представим f'(x) = 0
0=6x^2+14x+8
Решим ур-е относительно Х
6x^2+14x+8=0 | :2
3x^2+7x+4=0
D=b2-4ac = 7^2-4*3*4 = 1
x1,2= -b+-D/2a = -7+-1/2*3
x1= - 4/3
х2= -1
X∈(-∞;- 4/3)
X∈(- 4/3;-1)
max: - 4/3
min: -1
пусть b и с - положительные корни квадратного данного квадратного трехчлена, тогда по теореме Виета
b+c=-(-3/a)=3/a>0
bc=(5-a)/a>0
из первого неравенства имеем a>0
тогда из второго 5-a>0, 5>a, a<5
обьединяя 0<a<5
и получаем ответ
корни квадратного трехчлена y=ax²-3x+5-a положительны,если значение параметра а принадлежат множеству(0;5)
(проверка, что дискриминант больше 0 при найденных значениях - что соотвествует сушествованию двух корней трехчлена
D=9-a(5-a)=9-5a+a^2=(a^2-5a+6.25)+2.25>0 для любого а)