Question

Имеет ли решение система уравнений: 1) 2) 3)

Answer 1

1) $\displaystyle \left \{ {{x-y=4} \atop {3x-3y=6}} \right.$

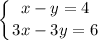
    Система решений не имеет, так как отношения коэффициентов при переменных равны, но не равны отношению свободных членов.

$\dfrac 13=\dfrac {-1}{-3} \neq \dfrac 46=\dfrac 23$

--------------------------------------------------------------

2)  $\displaystyle \left \{ {{x-1,5=-4} \atop {3y-2x=8}} \right.~~~\Rightarrow~~~\left \{ {{x=-2,5} \atop {3y-2x=8}} \right.$

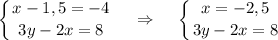
3y = 8 + 2·(-2,5);    3y = 3;     y = 1

Система имеет единственное решение  ( -2,5; 1)

Если предположить, что в условии опечатка : в первом уравнении потеряна переменная y, тогда система имеет вид

  $\displaystyle \left \{ {{x-1,5y=-4} \atop {3y-2x=8}} \right.$

  В таком виде система имеет бесконечно много решений, так как отношения коэффициентов при переменных равны отношению свободных членов.

$\dfrac 1{-2}=\dfrac {-1,5}3 = \dfrac {-4}8=-\dfrac 12$

Решения системы можно записать в виде  (1,5y-4; y)

--------------------------------------------------------------

3) $\displaystyle \left \{ {{9x+9y=18} \atop {x+y=2}} \right.$

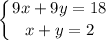
  Система имеет бесконечно много решений, так как отношения коэффициентов при переменных равны отношению свободных членов.

$\dfrac 91=\dfrac 91 = \dfrac {18}2=9$

Решения системы можно записать в виде  (x; 2-x)