а) Если на посл месте стоит 5, то сумма K=1+2+3+4+6+...+13 должна делится на 5
Но K=14*13/2-5=86, что не делится на 5, значит ответ нет
б)Чтобы на последнем месте было число m, нужно, чтобы 91-m делилось на m, то есть
91-m=km
значит m(k+1)=91
91=7*13
Значит m=1, m=7, m=13, m=91, так как числа от 1 до 13, то m=91 не подходит
значит ответ: 1,7,13. Осталось лишь показать что эти числа подходят.
в)Любые числа:
9,3,1,13,2,4,8,10,5,11,6,12,7
11,1,2,7,3,8,4,9,5,10,12,6,13
11,1,3,5,10,2,4,12,8,7,9,6,13
9,3,4,8,2,13,1,10,5,11,6,12,7
11,1,6,6,3,10,8,4,13,5,2,12,7
12,2,7,1,11,3,9,5,10,4,8,6,13
7,1,8,2,9,3,10,4,11,5,12,6,13
9,1,10,2,11,3,4,8,12,5,13,6,7
10,1,11,2,3,9,4,8,12,5,13,6,7
12,1,13,2,4,8,10,5,11,6,9,3,7
4,1,5,10,2,11,3,12,8,7,9,6,13
8,1,9,2,10,3,11,4,12,5,13,6,7
9,3,12,6,10,8,4,13,5,7,11,2,1
1)
ОДЗ: 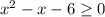 ⇒
⇒ 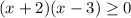 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
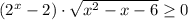 ⇔
⇔
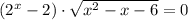 или
или 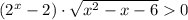
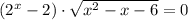 ⇒
⇒ 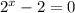 или
или 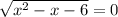 ⇒
⇒
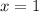 или
или  или
или 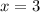
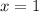 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 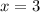
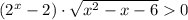 при
при ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
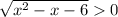 , тогда
, тогда 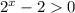 ⇒
⇒ 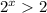 ⇒
⇒ 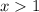
C учетом ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
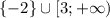
2)
ОДЗ: 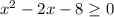 ⇒
⇒ 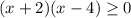 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
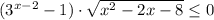 ⇔
⇔
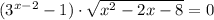 или
или 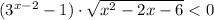
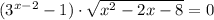 ⇒
⇒ 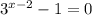 или
или 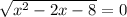 ⇒
⇒
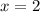 или
или  или
или 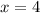
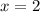 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 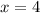
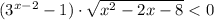 при
при ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
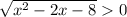 , тогда
, тогда 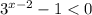 ⇒
⇒ 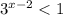 ⇒
⇒ 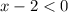
C учетом ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
![(-\infty;-2]\cup \{2\}](/tpl/images/1361/5355/83f26.png)
3)
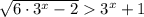
Так как 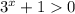 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
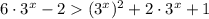
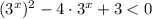
D=16-12=4
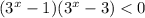
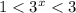
Показательная функция с основанием 3 возрастает
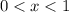
О т в е т. (0;1)
4)

Так как 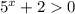 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
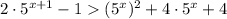
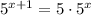
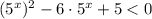
D=36-20=16
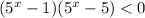
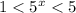
Показательная функция с основанием 5 возрастает
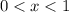
О т в е т. (0;1)
0.6^(x²+3x)>0.6^0 так как 0.6 <1, то знак неравенства меняется на противоположный
x²+3x<0
x(x+3)<0 x=0 x=-3 на числовой прямой наносим пустые точки 0 и (-3) , получаем 3 промежутка (-∞;-3) (-3;0) (0;∞). Подставить любые числа из промежутка в ваше уравнение х²+3х=0 и узнаете знаки на промежутках . Наш ответ: х∈(-3;0)
2)2^(-x²+3x)<4
2^(-x²+3x)<2² 2>1 знак неравенства не меняется
-х²+3x<2
-x²+3x-2<0 умножим все члены неравенства на (-1) , тогда знак неравенства поменяется)
x²-3x+2>0 x²-3x+2=0 D=9-4·2=1 x1=2 x2=1
(x-2)(x-1)>0
Наш ответ : (-∞;1) и (2;∞)
3) 8^((2х-1)\х)<4^((2x+3)\4) ОДЗ: Х≠0
2^((3(2x-1)\x)<2^((2(2x+3)\4)
(6x-3)\x<(4x+6)\4
(6x-3)\x-(4x+6)\4<0 приведём к общему знаменателю 4х:
(4(6x-3)-x(4x+6))\4x<0
(-4x²+18x-12)\4x<0 разделим на (-2) и знак неравенства поменяется
(2x²-9x+6)\2x>0 2x²-9x+6=0 D=81-48=33 √D=√33 x1=(9+√33)\4≈3.7 x2≈0.8
a) имеем систему : числитель и знаменатель имеют положительное значение :
2х>0 2(x-0.8)(x-3.7)>0
ответ:х∈(3.7;∞)
б) числитель и знаменатель---отрицательные, тогда ответ : х∈пустое множество решений.
ответ : х∈(3,7;∞)
4) 4^x-10·2^x+16<0
2^(2x)-10·2^x+16<0 вводим замену переменной: пусть 2^x=y x>0
y²-10y+16<0 y²-10y+16=0 D=100-64=36 √D=√36=6 y1=8 y2=2
Вернёмся к замене : a) 2^x=y1 2^x=2 x=1
b) 2^x=y2 2^x=8 2^x=2³ x=3
на числовой прямой отметить точки 1 и 3 ( пустые ), наш ответ : х∈(1;3)
5) 9^x-2·3^x≤3
3^(2x)-2·3^x-3≤0 вводим замену переменной : 3^x=y х>0
y²-2y-3≤0 y²-2y-3=0 D=16 y1=3 y2=-1
вернёмся к замене: а) 3^x=3 x=1
b) 3^x=-1 нет корней
ответ : х∈(0;1]