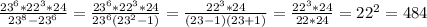
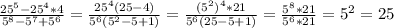
5) x=0, x= -2,5
6) f(1)=5
7) 500500
Объяснение:
5) 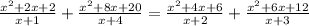
x ≠ -1, x ≠ -2, x ≠ -3, x ≠ -4
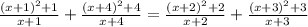
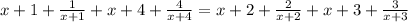
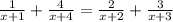
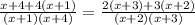
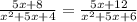
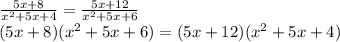
5x³+25x²+30x+8x²+40x+48=5x³+25x²+20x+12x²+60x+48
4x²+10x=0 ⇒ x=0, x= -2,5
6) 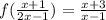
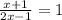
x+1=2x-1 ⇒ x= 2
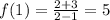
7) 1000·999-998·997+996·995-994·993-...+4·3-2·1
1000·999-998·997=(2+998)·999-998·997=2·999+998·999-998·997=
=2·999+2·998=2·(999+998)
996·995-994·993=(2+994)·995-994·993=2·995+994·995-994·993=
=2·995+2·994=2·(995+994)
...
4·3-2·1=(2+2)·3-2·1=2·3+2·3-2·1=2·3+2·2=2·(3+2)
1000·999-998·997+996·995-994·993-...+4·3-2·1= =2·(999+998)+2·(995+994)+...+2·3+2·2=
=2·(999+995+991+...+3)+2·(998+994+990+...+2)=
=2·(3+999):2·((999-3):4+1)+2·(2+998):2·((998-2):4+1)=
=1002·250+1000·250=250·2002=500500
Пусть х мер хлеба нужно дать первому человеку.
По условию второй получил на столько больше первого, на сколько третий получит больше второго, четвертый больше третьего, а пятый - больше четвертого.
Обозначим эту разницу как d, тогда
(х+d) мер хлеба нужно дать второму человеку;
(х+d)+d = (х+2d) мер хлеба нужно дать третьему;
(х+2d)+d = (х+3d) мер хлеба нужно дать четвертому;
(х+3d)+d = (х+4d) мер хлеба нужно дать пятому.
1) По условию все вместе получили 100 мер хлеба, получаем уравнение:
х+(х+d)+(х+2d)+(х+3d)+(х+4d)=100
5х+10d=100
Упростив, получаем первое уравнение:
х+2d=20
2) По условию первые два вместе получат в 7 раз меньше трех остальных, получаем уравнение:
7(х+х+d)=х+2d+х+3d+х+4d
Упростим:
14х+7d=3х+9d
11х=2d второе уравнение:
3) Из второго уравнения 2d=11х подставим в первое:
х+11х=20
12х=20
х= ²⁰/₁₂ = ⁵/₃ = 1 ²/₃
Подставим х = ⁵/₃ в уравнение х+2d=20 и найдем d.
⁵/₃+2d=20
2d=20 - ⁵/₃
2d= ⁵⁵/₃
d= ⁵⁵/₆ = 9 ¹/₆
1 ²/₃ мер хлеба первому;
1 ²/₃ + 9 ¹/₆ = 10 ⁵/₆ мер второму;
10 ⁵/₆ + 9 ¹/₆ = 20 мер третьему;
20 + 9 ¹/₆ = 29 ¹/₆ мер четвертому;
29 ¹/₆ + 9 ¹/₆ = 38 ²/₆ = 38 ¹/₃ мер пятому.
ответ. 1 ²/₃; 10 ⁵/⁶; 20; 29 ¹/₆; 38 ¹/₃ .