1.а) Область определения находим из системы неравенств
х+44>0; 2х-22>0;
х>-44;х>22/2⇒x∈(11;+∞).
4а) ㏒₃(х-4)+㏒₃(х+7)=㏒₃26; ОДЗ уравнения х больше 4, (х-4)(х+7)=26;
х²+7х-4х-28-26=0; х²+3х-54=0; По теореме, обратной теореме Виета, х₁=-9∉ОДЗ, не является корнем. х₂=6
4в) ㏒²₂х-㏒₂х-30=0; ОДЗ уравнения х∈(0;+∞) Пусть ㏒₂х=у, тогда у²-у-30=0; по теореме, обр. теореме Виета, у₁=-5; у₂=6 тогда ㏒₂х=-5; х=2⁻⁵; х=1/32 -входит в ОДЗ, корень.
㏒₂х=6; х=2⁶=64- входит в ОДЗ, корень.
5а)㏒₁/₅(22х-2)≥0
ОДЗ неравенства 22х-2>0; x>1/11
Заменим 0=㏒₁/₅1, т.к. основание логарифма меньше 1, то 22х-2≤1
22х≤3; х≤3/22; с учетом ОДЗ решением неравенства будет х∈(1/11;3/11)
,
, a 
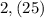
целая часть. У нас она равна 2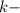
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25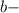
все цифры без периода в виде натурального числа. Их нет.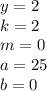
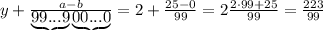
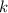подставляется количество 9, а под 
-количество нулей. У нас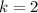 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между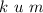 
не стоит знак умножения
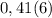
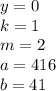
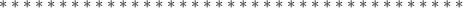
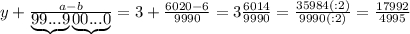
b1+b2+b3=14 => b1+b1q+b1q²=14 => b1(1+q+q²)=14
b1^2+b2^2+b3^2=84 => b1²*(b1q)²*(b1q²)²=84 => b1²(1+q²+q⁴)=84
{b1(1+q+q²)=14
{b1=√(84/(1+q²+q⁴) => b1=6/(q+q₂)
(6/(q+q₂))*(1+q+q²)=14
6+6q+6q²=14q+14q²
8q²+8q-6=0
4q²+4q-3=0
D=64
q₁=1/2
q₂=-3/2 - лишний корень, потому, что b1+b2+b3 - положительное чмсло)
q=1/2
b1(1+1/2+(1/2)²)=14
b1*7/4=14
b1=14*4/7
b1=56/7=8
ответ: b1=8
q=1/2
Проверка: 8+8*1/2+8*(1/2)²=14
8+4+2=14
14=14
8²+4²+2²=84
64+16+4=84
84=84