Фермер собрал с двух участков 50 т пшеницы. после внесения удобрений урожайность на первом участке повысилась на 30 %, а на втором – на 20 % , а потому фермер собрал с двух участков 63 т пшеницы. сколько тонн пшеницы собрал фермер с каждого участка первоначально?

👇

Ответ:

Dasa282

31.10.2022

Решение:
Обозначим первоначально собранный урожай пшеницы с первого участка за (х) тн, а со второго участка за (у) тн
Тогда первоначально фермер собирал пшеницы:
х+у=50 -первое уравнение
После внесения удобрений урожайность фермера на первом участке стала составлять:
х +х*30% :100%=х+0,3х=1.3х
на втором участке:
у +у*20% :100:=у+0,2у=1,2у
Общий урожай после внесения удобрений составил:
1,3х +1,2у=63-второе уравнение
х+у=50
1,3х+1,2у=63
Из первого уравнения найдём значение (х) и подставим во второе уравнение:
х=50-у
1,3*(50-у) +1,2у=63
65 -1,3 +1,2у=63
-0,1у=63-65
-0,1у= -2
у=-2 :0,1=20
х=50-20=30

ответ: Первоначально фермер собрал с первого участка 30т; со второго 20т

4,8(35 оценок)

Открыть все ответы

Ответ:

АйданкаТоктогулова

31.10.2022

На данном уроке мы рассмотрим методы решения системы линейных уравнений. В курсе высшей математики системы линейных уравнений требуется решать как в виде отдельных заданий, например, «Решить систему по формулам Крамера», так и в ходе решения остальных задач. С системами линейных уравнений приходится иметь дело практически во всех разделах высшей математики.

Сначала немного теории. Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени: без всяких причудливых вещей вроде и т.п., от которых в восторге бывают только участники математических олимпиад.

В высшей математике для обозначения переменных используются не только знакомые с детства буквы .
Довольно популярный вариант – переменные с индексами: .
Либо начальные буквы латинского алфавита, маленькие и большие:
Не так уж редко можно встретить греческие буквы: – известные многим «альфа, бета, гамма». А также набор с индексами, скажем, с буквой «мю»:

Использование того или иного набора букв зависит от раздела высшей математики, в котором мы сталкиваемся с системой линейных уравнений. Так, например, в системах линейных уравнений, встречающихся при решении интегралов, дифференциальных уравнений традиционно принято использовать обозначения

Но как бы ни обозначались переменные, принципы, методы и решения системы линейных уравнений от этого не меняются. Таким образом, если Вам встретится что-нибудь страшное типа , не спешите в страхе закрывать задачник, в конце-концов, вместо можно нарисовать солнце, вместо – птичку, а вместо – рожицу (преподавателя). И, как ни смешно, систему линейных уравнений с данными обозначениями тоже можно решить.

Что-то у меня есть такое предчувствие, что статья получится довольно длинной, поэтому небольшое оглавление. Итак, последовательный «разбор полётов» будет таким::

4,5(16 оценок)

Ответ:

Kokone143

31.10.2022

Линейное диофантово уравнение 7х+4у=123.
Если коэффициенты перед х и у простые числа, то это уравнение имеет решение в целых числах.
НОД(7,4)=1 ⇒ 7 и 4 - простые числа.
Подберём частное решение (x_0,y_0)

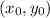. В этом уравнении это сделать не совсем просто, поэтому воспользуемся теоремой:
чтобы найти решение уравнения ах+ву=с при взаимно-простых а и в, нужно найти решение (x_0,y_0)

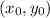уравнения ах+ву=1.
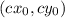Тогда числа (cx_0,cy_0)

составляют решение
уравнения ах+ву=с .
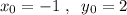7х+4у=1 ⇒ $x_0=-1\; ,\; \; y_0=2$ .

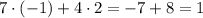
$7\cdot (-1)+4\cdot 2=-7+8=1$

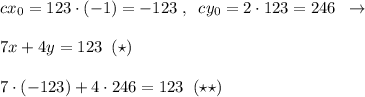
$cx_0=123\cdot (-1)=-123\; ,\; \; cy_0=2\cdot 123=246\; \; \to \\\\7x+4y=123\; \; (\star)\\\\7\cdot (-123)+4\cdot 246=123\; \; (\star \star )$

Из (*) вычтем (**) , получим:

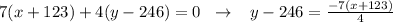
$7(x+123)+4(y-246)=0\; \; \to \; \; \; y-246= \frac{-7(x+123)}{4}$

Чтобы (у-246) было целым, надо чтобы (х+123) нацело делилось на 4, то есть х+123=4к ⇒ х=4к-123 , k∈Z .
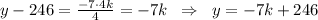
Тогда $y-246= \frac{-7\cdot 4k}{4} =-7k\; \; \Rightarrow \; \; y=-7k+246$

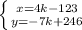ответ: $\left \{ {{x=4k-123} \atop {y=-7k+246}} \right.$ , $k\in Z.$