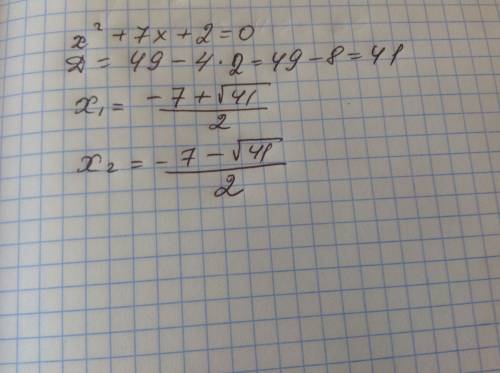
DenQ04a Ученый
б)
Строим таблицу, где первая колонка х, а вторая у.. .
ниже таблицы пишем
2х² + у = 4х - 3
2х² - 4х = -3 - у
При х=0, у=-3
х=1, у=-1
х=2, у=-3
х=3, у=-9
х=4, у=-19
(это пишем в таблицу)
Отмечаешь эти точки на координатной плоскости и соединяешь,
сначала имеет параболы, а от точки (2,-3) идет на низ прямая
в) xy = 8
y = 8/x
График - Гипербола
Строим таблицу
x≠0
x = -8, y = -1
x = -4, y = -2
x = -2, y = -4
x = -1, y = -8
x = 8, y = 1
x = 4, y = 2
x = 2, y = 4
x = 1, y = 8
Отмечаешь на координатной плоскости и проводишь Гиперболу.
Повторные независимые испытания. Схема Бернулли. Число попаданий - случайная величина, принимающая значения от 0 до 5. Найдем вероятности появления этих значений.
Вероятность Значения 0. Число сочетаний из 5(выстрелов всего) по 0(рассматриваемое значение) - это 1 - умножим на 0.5 в степени 0 и на 1-0.5 в степени 5-0. Получаем 0.03125. Это 1/32.
Вероятность значения 1. Число сочетаний из 5 по 1 - это 5 - умножается на 0.5 в степени 1 и на 1-0.5 в степени 5-1. Получаем 0.15625. Это 5/32.
Вероятность значения 2. Число сочетаний из 5 по 2 - это 10 - умножаем на 0.5 в степени 2 ина 1-0.5 в степени 5-2. Получаем 0.3125. Это 10/32.
Далее вероятности располагаются в обратном порядке в силу симметричности числа сочетаний и того, что 1-0.5 равно 0.5.
Ряд распределения:
0 1 2 3 4 5
0,3125 0,15625 0,3125 0,3125 0,15625 0,03125
Проверка. Сумма всех вероятностей равна 1.