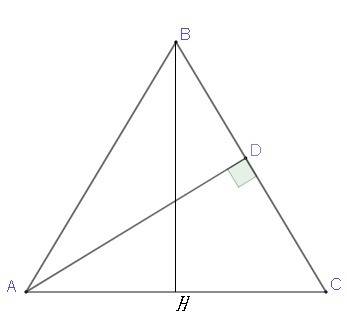
Дано: ABC - равнобедренный треугольник; AC = 12 см; AD = 9.6 см; AB=BC.
Найти: Рabc.
Из прямоугольного треугольника ADC по теореме Пифагора найдем CD
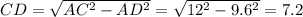см.
Пусть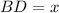 
, тогда 
.
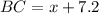Рассмотрим прямоугольный треугольник BHC найдем высоту BH к стороне основания AC; AH=CH=AC/2=6 см.
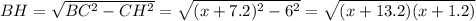
Площадь равнобедренного треугольника равна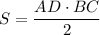 
, с другой стороны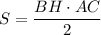 
Приравнивая площади, получим AD * BC = BH * AC.
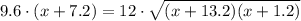
После возведения в квадрат обе части уравнения и упрощений с подобными членами вы должны получить следующее квадратное уравнение
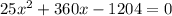
Корни которого: 
- не удовлетворяет условию
см
Тогда 
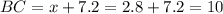см
Pabc = AB + BC + AC = 10 + 10 + 12 = 32 см
ответ: 32 см.
а) х2+5х-14=(х-2)(х+7);
х2+5х-14=0;
д=25-4*(-14)=25+56=81;
х1=(-5+9)/2=4/2=2;
х2=(-5-9)/2=-14/2=-7;
б)16х2-14х+3=16(х-0,5)(х-0,375);
16х2-14х+3=0
д=(-14)2-4*16*3=196-192=4;
х1=(14+2)/32=16/32=0,5;
х2=(14-2)/32=12/32=0,375;
в)(3у2-7у-6)/(4-9у2)=3(у-3)(у+2/3)/-9(у-2/3)(у+2/3)=3(у-3)/(6-9у)=
(3у-9)/(6-9у)=3(у-3)/3(2-3у)=(у-3)/(2-3у);
3у2-7у-6=(у-3)(у+2/3);
3у2-7у-6=0
д=49-4*3*(-6)=49+72=121;
у1=(7+11)/6=18/6=3;
у2=(7-11)/6=-4/6=-2/3;
4-9у2=-9(у-2/3)(у+2/3);
4-9у2=0
9у2=4
у1=4/9=2/3;
у2=-2/3.
8x - 6x=20+10
2x=30
x=30:2
x=15