Объяснение:
1) построим графики y=3x² и у=12
из точки пересечения графиков проведем отрезки перпендикулярно оси ОХ
точки пересечения перпендикуляра к оси ОХ определяют отрезок на оси ОХ являющийся решением
х∈[-2;2]
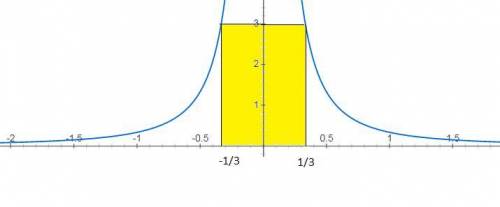
2) построим график y=1/(3x)²
и у=3
из точки пересечения графиков проведем отрезки перпендикулярно оси ОХ
точки пересечения перпендикуляра к оси ОХ определяют отрезок на оси ОХ являющийся решением
х∈(-1/3;1/3)

В решении.
Объяснение:
1) Решить неравенство:
3х² <= 12
Решить как квадратное уравнение:
3х² = 12
х² = 4
х = ±√4
х = ± 2.
х = -2 и х = 2 - точки пересечения параболой оси Ох.
Построить график у = 3х² - 12
Определить по графику, при каких значениях х у <= 0.
По графику ясно видно, что у <= 0 при х от -2 до 2.
Решение неравенства: х∈[-2; 2], пересечение.
Неравенство нестрогое, скобки квадратные.
2) Решить неравенство:
х²/3 > 3
Решить как квадратное уравнение:
х²/3 = 3
х² = 9
х = ±√9
х = ± 3.
Построить график у = х² - 9.
Определить по графику, при каких значениях х у > 0.
По графику ясно видно, что у > 0 при х от -∞ до -3 и от 3 до + ∞.
Решение неравенства: х∈(-∞; -3)∪(3; +∞), объединение.
Все неотрицательные целые числа - натуральные. Кроме нуля. Ноль - целое число.
Это числа счёта (на руке 5 пальцев, их можно посчитать) .
Числа 1, 2, 3, 4, 5, 6, 7 - натуральные. Принадлежат промежутку от 0 до 7 включительно не включая ноль. То есть числа 1, 2, 3, 4, 5, 6, 7 входят в промежуток [1;7]. Именно в квадратных скобках. ( В круглых мы бы исключили крайние чила. )