№1 (а)
ответ: -\frac{4}{3}" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=x%20%3E%20-%5Cfrac%7B4%7D%7B3%7D" title="x > -\frac{4}{3}">
№1 (б)
№2 (а)
-4} \atop {x\leq -2.5}} \right." class="latex-formula" id="TexFormula6" src="https://tex.z-dn.net/?f=%5Cleft%20%5C%7B%20%7B%7Bx%3E-4%7D%20%5Catop%20%7Bx%5Cleq%20-2.5%7D%7D%20%5Cright." title="\left \{ {{x>-4} \atop {x\leq -2.5}} \right.">
№2(б)
\frac{36}{5}" class="latex-formula" id="TexFormula10" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
ответ: \frac{36}{5}" class="latex-formula" id="TexFormula12" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
а)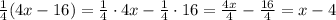
б)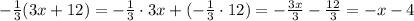
в) (2х-3у)·(-3)=-3(2х-3у)=-3·2x-3·(-3y)=-6x+9y
г) 2m(m-n)=2m·m-2m·n=2m²-2mn
д) 2x(a+3b-c)=2x·a+2x·3b-2x·c=2ax+6bx-2cx
е) -c(x-2y+3z)=-c·x-c·(-2y)-c·3z=-cx+2cy-3cz