Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности. Периметр шестиугольника равен 48 => сторона равна 48/6=8; то есть радиус описанной окружности равен 8. Если вписать в эту окружность квадрат то его диагональ - это диаметр окружности - то есть 16, стороны квадрата пусть будут х, тогда по теореме пифагора (диагональ и две стороны квадрата образуют прямоугольный треугольник - гипотенуза это диагональ квадрата а кататы равны между собой - стороны квадрата)
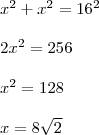
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности. Периметр шестиугольника равен 48 => сторона равна 48/6=8; то есть радиус описанной окружности равен 8. Если вписать в эту окружность квадрат то его диагональ - это диаметр окружности - то есть 16, стороны квадрата пусть будут х, тогда по теореме пифагора (диагональ и две стороны квадрата образуют прямоугольный треугольник - гипотенуза это диагональ квадрата а кататы равны между собой - стороны квадрата)
в экстремальных точках y`=0
y`=2x*e^x+x^2*e^x=e^x(2x+x^2)=0
e^x>0
x^2+2x=x(x+2)=0
x1=0; x2=-2
второй корень в указанный интервал не входит
нахожу у на концах интервала и в x=0
y(-1)=e^(-1)=1/e≈1/2.72=0.37
y(0)=0
y(2)=4e^2
минимум y(0)=0; максимум y(2)=4e^2