Решить графически систему уравнений:
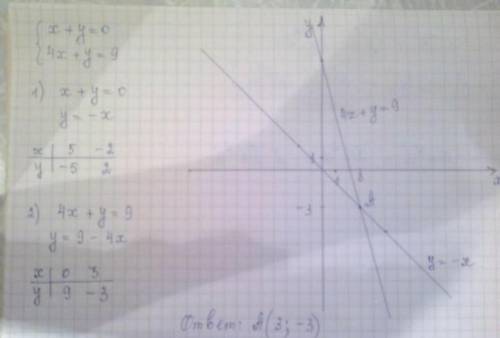
1)
у = х + 6
у = 2 - 1/3 х
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у = х + 6 у = 2 - 1/3 х
Таблицы:
х -1 0 1 х -3 0 3
у 5 6 7 у 3 2 1
Координаты точки пересечения прямых (-3; 3).
Решение системы уравнений (-3; 3).
3)
Надо построить графики двух прямых:
1) х= -1 ( красный график) (прямая параллельная оси ОУ, проходящая через точку (-1;0) на оси ОХ)
2) приведём уравнение к виду y=kx+b
2x+y=3 → у= -2х+3 ( график синий)
заполним таблицу точек (для построения прямой достаточно двух)
х 0 2
у 3 -1
Координаты точки пересечения - решение данного уравнения:
х= -1, у= 5
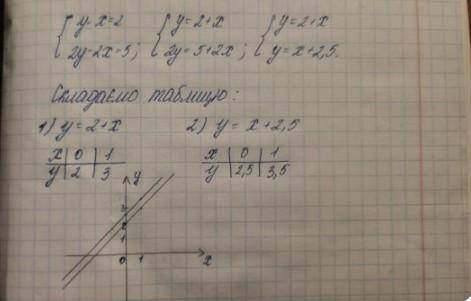
Объяснение:
как убножить дробь на дробь?нам нужно числитель умножить на числитель, а знаменатель на знаменатель!
1 дробь: числитель 2•4=8 знанатель 3•5=15
и у нас получается дробь 8/15. Всё и так со стальными решаешь именно умножения
ДЕЛЕНИЕ:.МЫ ПЕРВУЮ ДРОБЬ ОСТАВЛЯЕМ А ВТОРУЮ ПРОСТО ПЕРЕВОРАЧИВАЕШЬ И МЫ ДЕЛЕНИЕ ЗАМЕНЯЕМ НА УМНАЖЕНИЕ:
2/3:5/7=2/3•7/5 И ВСЁ ТЕПЕРЬ УМНАЖЕНИЕ КАК ОБЫЧНО 2•7=14, 3•5=15 и получается 14/15доробь
Под ж) там 4 представляешь как 4/1 и решаешь как обычное деление первую оставляешь а другую переворачиваешь под з) тоже самое под г) там эту дробь убнажаешь два раза потому что там стоит квадрат
Начну сначала.
Полная запись функции выглядит так: y(x)=-x^5. Это означает, что подставив в качестве аргумента функции значение x, мы получим численное значение y.
Полная запись координат точки на графике выглядит так: (x=2;y=32). То есть, взяв из примера первый аргумент x мы получим значение y. Задача заключается в том, чтобы сравнить полученное значение y после подстановки x в функцию с имеющимся.
Немного комментариев про исходную функцию y(x)=-x^5. Так как знак - не включен в степень, то любой аргумент функции из положительных чисел дат отрицательное число, а с отрицательное наоборот - положительное, так как любое отрицательное число в нечетной степени дает число с тем же знаком минус. Минус умноженный на минус даст плюс.
Решение
1) y(2)=-2^5=-32 - Не подходит
2) y(-32)=-(-32)^5=33554432 - Не подходит
3) y(-2)=-(-2)^5=32 - Не подходит
4) y(2)=-2^5=-32 - Подходит
ответ: 4
A2.
График функции y(x)=-x^27.
По данной функции можно сразу сказать, что, как и в задании, положительное значение аргумента x будет давать отрицательное значение y, а отрицательное значение аргумента x будет давать положительное значение y, так как минус не под степенью, а сама степень - нечетное число.
Сделав такое заключение можно прийти к выводу, что задавая положительные значения x, график функции сразу пойдет в 4 четверть (значение y будет отрицательным), а задавая отрицательное значение x, график функции сразу пойдет во 2 четверть.
ответ: 2