Возьмем ваше же уравнение
lx+2l+lxl+lx-2l=4
Левую и правую части уравнения рассматриваем как функции.
f(x)=lx+2l+lxl+lx-2l и g(x)=4
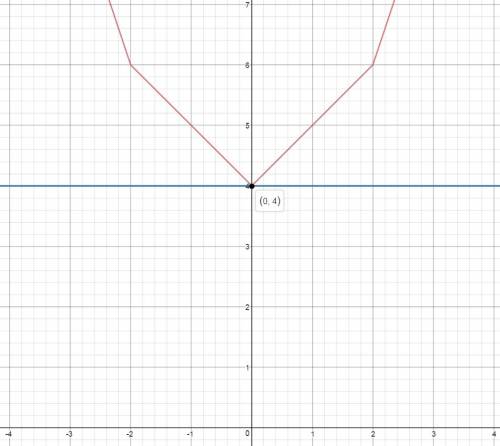
С g(x) все понятно. Это прямая y=4, параллельна Ox.
С f(x) разбираемся. Это кусочная функция. Найдем нули подмодульных выражений:
x+2=0 ⇒ x=-2, x-2=0 ⇒ x=2, x=0.
Имеем интервалы (-∞; -2); [-2; 0); [0; 2); [2; +∞). Запишем равносильный переход:
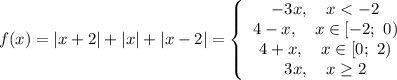
Построение графика на этом этапе элементарно. Из системы можно видеть, что функция f(x) четная. Достаточно построить или левую или правую ее часть, остальное отзеркалить. Готовый рисунок приложен.
350000 и -335000 соответственно.
Объяснение:
Пусть x и y - вклады на первый и второй счёт соответственно. Причём y=15000-x.
Тогда через год суммы вкладов увеличились на 0.07*x и 0.1*y соответственно. Причём 0.07*x + 0.1*y = 12000.
Подставим:
0.07*x + 0.1*y = 12000
0.07*x + 0.1*(15000-x) = 12000
1500-0.03x=12000
0.03x=10500
x=350000.
Тогда y = 15000-x = -335000.
Пояснение:
Деньги можно не только вкладывать, но и брать в кредит у банка. По условиям задачи величина процентных денег слишком велика, чтобы получить её за год с маленькой суммы (15000) и низких процентов(7 и 10). Задача имела бы натуральное решение, либо если бы сумма вкладов была меньше, либо если бы проценты были больше, раз в 10.