1)5х+7=9
х=0,4
2)2х+5+8=1
2х+13=1
2х=1-13
2х=-12
х=-6
3) х^2+1=x+5
x^2-x-4=0
D=(-1)^2-4*1*(-4)=1+16=17
x1=1+корень из 17/2
х2=1-корень из 17/2
4)5+3х=2х+1
х=-4
5) х+4+3х+1=9
4х=4
х=1
2) 4+7=11 (ч) - общее время в пути.
3) 640-35=605 (км)
4) 605:11=55 (км/ч) - скорость машины.
5) 55+5=60 (км/ч) - скорость поезда Предположим, что скорость поезда х км/ч, тогда скорость машины (х-5) км/ч, также из условия задачи известно, что за 4 часа езды на машине и 7 часов езды на поезде туристы проехали 640 км
согласно этим данным составим и решим уравнение:
4(х-5)+7х=640
4х-20+7х=640
11х-20=640
11х=640+20
11х=660
х=660:11
х=60 (км/ч) - скорость поезда.
х-5=60-5=55 (км/ч) - скорость машины Предположим, что скорость машины х км/ч, тогда скорость поезда (х+5) км/ч, также из условия задачи известно, что за 4 часа езды на машине и 7 часов езды на поезде туристы проехали 640 км
согласно этим данным составим и решим уравнение:
4х+7(х+5)=640
4х+7х+35=640
11х+35=640
11х=640-35
11х=605
х=605:11
х=55 (км/ч) - скорость машины.
х+5=55+5=60 (км/ч) - скорость поезда Предположим, что скорость поезда х км/ч, а скорость машины у км/ч, также из условия задачи известно, что за 4 часа езды на машине и 7 часов езды на поезде туристы проехали 640 км, а зная, что скорость поезда больше скорости машины на 5 км/ч
составим и решим систему уравнений:

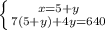
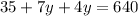

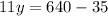
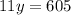
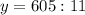
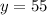 (км/ч) - скорость машины.
(км/ч) - скорость машины.
 (км/ч) - скорость поезда.
(км/ч) - скорость поезда.
ответ: скорость поезда 60 км/ч.
Проверка:
1) 55·4=220 (км) - проехали туристы на машине.
2) 60·7=420 (км) - проехали туристы на поезде.
3) 220+420=640 (км) - весь путь.
1) M = {11k + 7, где к = 1,2,3,4,5,6,7,8} = {11,18,25,32,39,46,53,60,67,74,81,88}
2) М = n^2, n = 1,2,3,...,9. M = {квадраты всех чисел от 1 до 9}
3) (x,y,z), где x - 1-я монета, y - 2-я монета, z - 3-я монета: x+y+z < 6 => среди x, y и z не может быть ни одной 5-ки, а также больше двух двоек.
a) Ноль двоек: (1,1,1) b) Одна двойка: (1,1,2),(1,2,1),(2,1,1) c) Две двойки: (1,2,2),(2,1,2),(2,2,1). Итак: (1,1,1),(1,1,2),(1,2,1),(2,1,1),(1,2,2),(2,1,2),(2,2,1)
4) (x,y), где x - число очков выпавших на 1-й кости, y - число очков выпавших на 2-й кости: |x-y| < 2 => (1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),(5,4),(5,5),(5,6),(6,5),(6,6) - все пары (x,y) такие, что |x-y| < 2. Всего таких пар n = 16.
5) Двухзначные числа: 10,11,12,13,...,99. Всего таких чисел N = 99-10 = 89. Двухзначные числа, которые делятся на 13: m = 13k, k = 1,2,3,4,5,6,7. Всего таких чисел n = 7. Отсюда, искомая вероятность p = 7/89
|5x+7|=9
5х+7=9 5х+7=-9
5х=9-7 5х=-9-7
5х=2 5х=-16
х1=0,4 х2=-3,2
ответ: х1=0,4, х2=-3,2.
||2x+5|-8|=1
|2x+5|-8=1 |2x+5|-8=-1
|2x+5|=1+8 |2x+5|=-1+8
|2x+5|=9 |2x+5|=7
2x+5=9 2x+5=-9 2x+5=7 2x+5=-7
2х=9-5 2х=-9-5 2х=7-5 2х=-7-5
2х=4 2х=-14 2х=2 2х=-12
х=4:2 х=-14:2 х=2:2 х=-12:2
х1=2 х2=-7 х3=1 х4=-6
ответ: х1=2, х2=-7, х3=1, х4=-6
|x^2-1|=|x+5|
x^2-1=x+5
x^2-x-1-5=0
x^2-x-6=0
по теореме Виета:
х1=3 х2=-2
овет: х1=3, х2=-2
|5-3x|=2x+1
5-3х=2х+1 5-3х=-(2х+1)
5-1=2х+3х 5-3х=-2х-1
4=5х 5+1=-2х+3х
х=4:5 х2=6
х1=0,8
ответ: х1=0,8, х2=6.
В последнем не уверена, как правильно записать:
|x-4|+|3x+1|=9
|x-4|=9-|3x+1|
х-4=-9+|3х+1|
x-4+9=|3x+1|
|3x+1|=x+5
3x+1=x+5 3x+1=-(x+5)
3х-х=5-1 3х+1=-х-5
2х=4 3х+х=-5-1
х=4:2 4х=-6
х1=2 х=-6:4
х2=-1,5
ответ: х1=2, х2=-1,5.