Искомое количество чисел найдем так: от общего количества четырехзначных чисел с неповторяющимися цифрами отнимем количество четырехзначных чисел с неповторяющимися нечетными цифрами.
Итак, ищем общее количество четырехзначных чисел с неповторяющимися цифрами.
На первом месте может стоять любая из цифр от 1 до 9 (9 вариантов). На втором месте - любая из 9 (8 неиспользованных на предыдущем шаге + цифра "0"), на третьем - любая из 8 оставшихся, на четвертом - любая из 7 оставшихся. Тогда общее количество чисел:
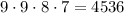
Ищем количество четырехзначных чисел с неповторяющимися нечетными цифрами.
На первом месте может стоять любая из нечетных цифр (5 вариантов). На втором месте - любая из 4 оставшихся, на третьем - любая из 3 оставшихся, на четвертом - любая из 2 оставшихся. Тогда общее количество чисел:
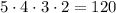
Значит, искомое количество четырехзначных чисел с неповторяющимися цифрам, в записи которых есть хотя бы одна чётная цифра:
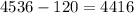
ответ: 4416 чисел
8х²+4х-6х-3= 5+8х²+2х-12х-3
8х²-2х-3=8х²-10х+2
8х²-2х-8х²+10х=2+3
8х=5
х=5/8
Проверим:
(4 *5/8 - 3) (2* 5/8 + 1) = 5+ ( 2 *5/8 - 3) (4 *5/8 +1 )
(5/2 - 6/2)( 5/4 +4/4) = 5+ ( 5/4 - 12/4 )( 5/2 +2/2)
(-1/2) * (9/4) = 5+ (-7/4) * (7/2)
-9/8 = 5+ (-49/8)
-1 1/8 = 5 - 6 1/8
- 1 1/8 = - 1 1/8