Составим арифметическую прогрессию и вычислим сколько трехзначных цифр делятся на 51.
а(1)=102, d=51, a(n)=969(последнее число, делящееся на 51)
a(n)=a(1)+d(n-1)
969=102+51n-51
51n=969-51
51n=918
n=18
Известно, что трехзначных чисел 900=)
Следовательно, вероятно равна Р(А)=18/900=1/50 (благоприятные случаи делим на всевозможные)
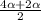sin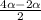
=2cos3α*sinα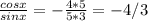
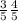=-24/25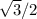
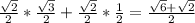
а) 5,5
б) 12,35
в) 11,5
г) 12,15
Объяснение:
a) Амплитуда (размах) — разность между наибольшим и наименьшим элементами
б) Медиана — полусумма средних элементов упорядоченной последовательности.
Данная последовательность состоит из 10 элементов (чётное количество), следовательно, средние элементы — пятый и шестой.
в) Мода — элемент, имеющий наибольшую частоту, т. е. 11,5 см
(встречается в таблице два раза).
г) Чтобы вычислить среднее арифметическое, необходимо сумму всех чисел разделить на их количество (на 10).
Валя выбрала трехзначное число, значит это числа от 100 до 999, следовательно
Вероятность=18/900=1/50
вот логика
вероятность = колличество правильных вариантов/колличество возможных вариантов.
определить числа на которые 3значное число делиться на 51 без остатка
получаем что 1-не подходит,
2 подходит так как 2*51=102... и так далее последнее 3значное число это 51*19=969. далее уже при умножении 51 на какое либо число после 19 пойдут четырехзначные числа.
значит кол-во всех трехзначных чисел : 999-100+1=900
и получаем 18/900, вот при сокращении получем 1/50
Вот все решение)))