рассмотрим наше уравнение:
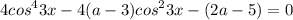
выполним замену cos²3x=t; t≥0
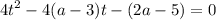
чтобы уравнение имело хотя бы один корень надо чтобы D≥0
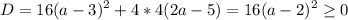
Это неравенство выполняется для любых a
тогда проверим корни, необходимо чтобы t≥0
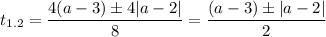
рассмотрим первый корень
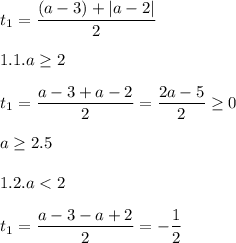
значит при а≥2.5 мы получим один положительный корень (относительно t)
проверим второй корень
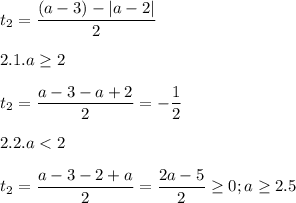
тут положительных корней не получим.
значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5
выполним обратную замену
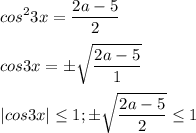
рассмотрим положительный корень
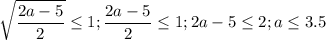
рассмотрим отрицательный корень
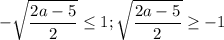
выполняется для всех а≥2.5
Собираем все вместе 2,5≤а≤3,5
1)2cosx+1=0, cosx=-1/2, x=+-2π/3+2πk, k∈z
2sinx-√3=0, sinx=√3/2, x=(-1)^k*π/3+kπ,k∈z
2) cosx(2-3sinx)=0,sinx=0,x=πk,k∈z
2-3sinx=0, sinx=2/3, x=(-1)^k arcsin2/3+πk,
3)sinx(4sinx-3)=0, sinx=0, x=πk,k∈z
4sinx-3=0 sinx=3/4, x=(-1)^karcsin3/4+πk,k∈z
4)(sin^2(x)=1/2,x=+-π/4+πk,k∈z.
5)6sin^2(x)+sinx-2=0,Sinx=t, 6t^2+t-2=0 , его корни t1=-2/3,t2=1/2,
sinx=-2/3,x=(-1)^(k+1)arcsin2/3+πk,k∈z, sinx=1/2,x=(-1)^kπ/6+πk,k∈z.
6) 3cos^2(x)-7sinx-7=0,Заменим косинус на синус получим
3sin^2(x)+7sinx+4=0, его корни sinx=-8/6- корней нет, sinx=-1, x= -π/2+2πk,k∈z
Объяснение:
тут надо расписать 12 член прогресси и тогда найдем 1й
А12=А1+11d
-24=А1+44
А1=-24-44
А1=-68