Площадь фигуры может быть вычислена через определённый интеграл.
График функции y=3x² - 2 - квадратная парабола веточками вверх. Вершина параболы находится в точке А(0; -2). Парабола пересекает ось х в двух точках:
х₁ = -√2/3 ≈ -0,816
х₂ = √2/3 ≈ 0,816
Найдём пределы интегрирования
При х = 1 y=3x² - 2 = 1
Эта точка находится правее нуля функции в точке х₂ ≈ 0,816, т.е. в области положительных у, поэтому нижний предел х = 1, ну, а верхний предел, естественно, х = 2.
Интегрируем: ∫(3x² - 2)dx = x³ - 2x.
Подставляем пределы:
S = (2³ - 2·2) - (1³ - 2·1) = 4+1 = 5
ответ: Площадь фигуры равна 5
(ab – a – 4)² + (ab – b – 3)² = 0
В левой части равенства находится сумма квадратов. Поскольку никакое действительное число при возведении в квадрат не может дать отрицательный результат, слагаемые в левой части либо нулевые, либо положительные. В таком случае сумма этих слагаемых равна нулю только тогда, когда каждое из слагаемых равно нулю.
Получаем систему из двух уравнений:
ab – a – 4 = 0
ab – b – 3 = 0
Из первого уравнения выразим b=(a + 4)/a и подставим полученное значение во второе уравнение:
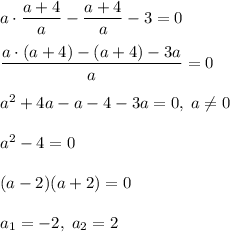
Подставим полученные значения a в первое уравнение и найдем b:
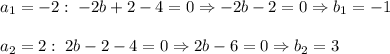
ответ: a₁ = –2, b₁ = –1; a₂ = 2, b₂ = 3.