Пусть х руб. - цена детского билета, у руб. - цена взрослого билета. Составим систему уравнений по условию задачи:
{2х + у = 315
{3х + 2у = 565
- - - - - - - - - - - -
Вычтем из второго уравнения первое:
(3х - 2х) + (2у - у) = 565 - 315
х + у = 250
у = 250 - х
- - - - - - - - - - - -
Подставим значение у в любое уравнение системы
2х + 250 - х = 315 3х + 2 · (250 - х) = 565
2х - х = 315 - 250 3х + 500 - 2х = 565
х = 65 3х - 2х = 565 - 500
х = 65
- - - - - - - - - - - -
у = 250 - 65
у = 185
ответ: детский билет стоит 65 рублей,
а взрослый билет стоит 185 рублей.
Проверка:
2 · 65 + 1 · 185 = 130 + 185 = 315 руб. - заплатила первая семья
3 · 65 + 2 · 185 = 195 + 370 = 565 руб. - заплатила вторая семья
ответ: 4132 .
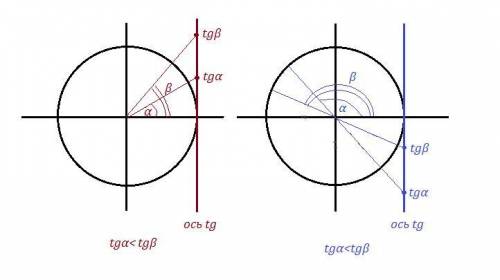
Угловой коэффициент прямой k - это тангенс угла наклона ( tgα ) прямой к положительному направлению оси ОХ.
Все острые углы α имеют положительный tgα>0 , а тупые углы - отрицательный tgα<0 .
Прямые 1 и 4 наклонены под острым углом, значит их угловые коэффициенты положительны ( k₁>0 , k₄>0 ) . А прямые 2 и 3 наклонены под тупым углом к оси ОХ , значит их угловые коэффициенты отрицательны ( k₂<0 , k₃<0 ) .
Все положительные числа больше отрицательных . Теперь сравним между собой k₁ и k₄ , а также k₂ и k₃ .
Чем больше острый угол, тем больше tg этого угла , значит k₄>k₁ .
Чем меньше тупой угол, тем меньше tg этого угла, значит k₃>k₂ .
Окончательно получаем: k₄>k₁>k₃>k₂ .