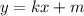 : если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором
: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 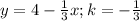 . С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения
. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 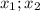 , два произвольных числа, но
, два произвольных числа, но 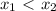 . Пусть мы имеем функцию
. Пусть мы имеем функцию  , тогда вычисляем значения функции в этих двух точках, имеем
, тогда вычисляем значения функции в этих двух точках, имеем 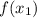 и
и 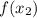 , так вот, если
, так вот, если  , тогда функция возрастающая, если же
, тогда функция возрастающая, если же 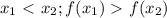 , то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)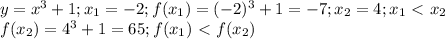 , т.е. функция возрастающая. А вот задание с
, т.е. функция возрастающая. А вот задание с 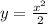 не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной)
не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 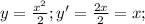 . Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка):
. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 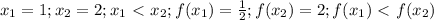 , функция возрастает, что и требовалось доказать.
, функция возрастает, что и требовалось доказать.
Дано:
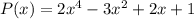

Найти 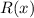 - остаток от деления
- остаток от деления 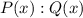
Решение.
1) Для начала разложим многочлен 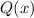 на множители, для этого решим уравнение:
на множители, для этого решим уравнение:
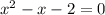
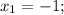

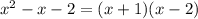
2) Так как данный многочлен 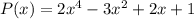 делится на
делится на 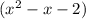 с остатком, то представим его в виде
с остатком, то представим его в виде
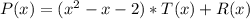
где
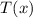 - неполное частное;
- неполное частное;
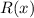 - искомый остаток.
- искомый остаток.
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
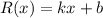
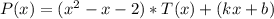
3) Подставим в равенство 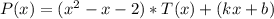 первый корень
первый корень 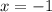 и получим:
и получим:
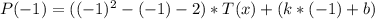
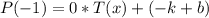
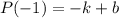
Вычислим 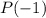 .
.
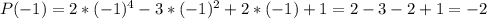
Так как 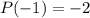 , то
, то
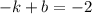 =>
=> 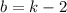
4) Аналогично решаем и со вторым корнем 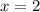 .
.
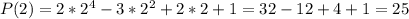
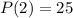
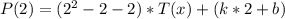
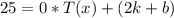
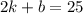
5) Подставим 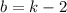 в полученное уравнение:
в полученное уравнение:
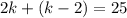
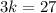
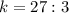
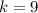
6) 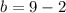
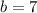
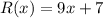 - искомый остаток.
- искомый остаток.
ответ: 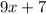
sin(p/2-a)cos(p+a)/ctg(p+a)tg(3p/2-a) =
= [cosa * (- cosa)] / [ctga * ctga] = - cos²a / (cos²a/sin²a) = - sin²a