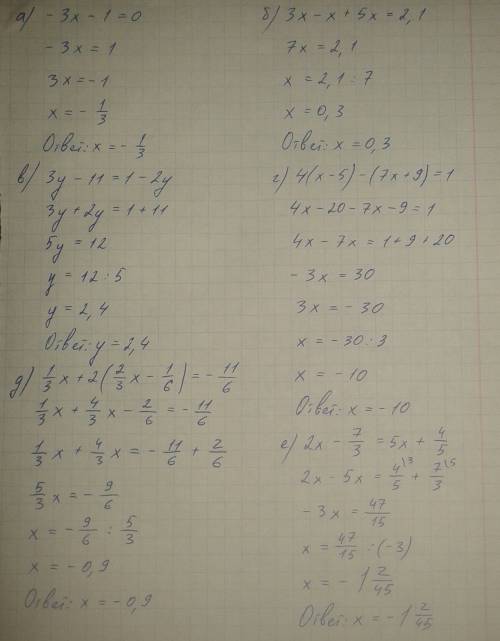
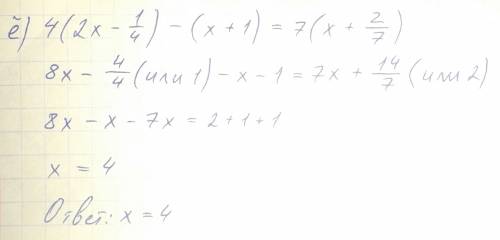
Решить систему линейных уравнений методом подстановки и методом сложения:
{
y
+
2
x
=
1
y
−
x
=
3
Решение методом подстановки.
{
y
+
2
x
=
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
(
−
2
x
+
1
)
−
x
=
3
⇒
{
y
=
−
2
x
+
1
−
3
x
−
2
=
0
⇒
{
y
=
−
2
x
+
1
x
=
−
2
3
⇒
{
y
=
7
3
x
=
−
2
3
y
=
2
1
3
;
x
=
−
2
3
Решение методом сложения.
{
y
+
2
x
=
1
y
−
x
=
3
Вычитаем уравнения:
−
{
y
+
2
x
=
1
y
−
x
=
3
(
y
+
2
x
)
−
(
y
−
x
)
=
1
−
3
3
x
=
−
2
x
=
−
2
3
Подставиим найденную переменную в первое уравнение:
(
−
2
3
)
+
2
x
=
1
y
=
7
3
y
=
2
1
3
;
x
=
−
2
3
Объяснение:
ответ:
9а во второй степени + (7а во второй степени - 2а - (а во второй степени - 3а))=9а во второй степени = 9*9=81; +7а во второй степени=7*7=49: -
если а =1 то а во второй степени = 1
если а=2 то а во 2 степени = 4
если а 847 то а во второй степени = 717409
если а 939846382469823649823 то а во 2 степени = 883311222641614039149097242705004927931329
ну а если а 214351850748450383906929029648290036511493291095893447739025 то а во 2 степени = 45946715919285949407498907818061086336294597480997799164546820374726775942238249523351663057736366081827118884507950625
объяснение: 4594671591928594940749890781806108633629459748099779916454682037472677594223824952335166305773636608182711888450795062545946715919285949407498907818061086336294597480997799164459467159192859494074989078180610863362945974809977991645468203747267759422382495233516630577363660818271188845079506254594671591928594940749890781806108633629459748099779916454682037472677594223824952335166305773636608182711888450795062545946715919285949407498907818061086336294597480997799164546820374726775942238249523351663057736366081827118884507950625