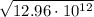. Чтобы извлечь его из под корня, нужно извлечь из под корня 
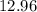, а затем 
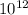. Если степень четная, то уменьшаем ее в 2 раза, если нечетная, то из под корня полностью число в этой степень извлечь нельзя.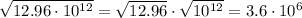 
![\sqrt[n]{a^m} = a^{\frac{m}{n}}](/tpl/images/0561/7515/fd5e1.png)
![a^{\frac{1}{2}} = \sqrt[2]{a^1} \\ a^{\frac{4}{2}} = \sqrt[2]{a^4} \\ a ^ {\frac{3}{6}} = \sqrt[6]{a^3} \\](/tpl/images/0561/7515/b4cce.png)
![\sqrt[2]{(10^6)^1}](/tpl/images/0561/7515/7734e.png)
. 
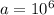возведено в 1 степень, то есть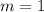
, степень корня — 2 (
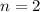). Перейдем от записи в виде корня к записи в виде степени:![\sqrt[2]{(10^6)^1} = (10^6)^{\frac{1}{2}}](/tpl/images/0561/7515/3f459.png)
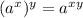, тогда: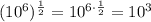
ответ: Не хватит
Объяснение: Сначала нужно посчитать площадь образца и шали, тоесть 10*10=100см², 170*70=11900см², далее нужно поделить обе площади, тоесть 11900:100=119см², теперь нужно умножить 119 на то число пряжи, которое было потрачено на образец, тоесть: 119*23=2737м, и чтобы окончательно понять, хватит ли пряжи или нет, нужно узнать, сколько всего пряжи есть у Марины Алексеевны, для этого 350*6=2100м, под итог, ей не хватит пряжи, потомучто число нужной пряжи больше чем то число пряжи, которое есть у Марины Алексеевны
cos²x=1-sin²x
3-3sin²x-sin²x+4sinx=0
-4sin²x+4sinx+3=0
t=sinx -1≤t≤1
-4t²+4t+3=0
D=16+48=64 √D=8
t₁=(-4+8)/(-8)= -(1/2)
t₂=(-4-8)/(-8)=12/8 не подходит т.к. (12/8)>1
sinx=-(1/2)
x=(-1)ⁿ(-π/6)+nπ, n∈Z