Объяснение:
1. При каких условиях число a> b? Если a-b >0 т.е положительна разность Как это обозначается? a-b >0
2. Покажите знаки строгого и нестрогого неравенств. ≤ ≥
3. Какие свойства числовых неравенств вы знаете?
Если a>b и b>c , то a>c .
Если a>b , то a+c>b+c .
Если a>b и k>0 , то ak>bk .
Если a>b и k<0 , то ak<bk .
4. Что вы понимаете под доказательством неравенства?
Преобразование частей по правилам к очевидному результату
5. Назовите методы доказательства неравенств и раскройте их смысл.
С известным перенести в одну сторону с неизвестным в другую, привести подобные члены и сделать выводы.
6. Что значит решить неравенство? Найти все его решения или установить , что их нет
7. Какие неравенства называются равносильными? которые имеют одни и те же решения.
8. Какие неравенства называются квадратными? неравенство вида ах²+вх+с (≤,≥,>,<)0
9. Объясните решение неравенств методом интервалов. Нужно квадратичный трехчлен представить в виде произведения, найти нули квадратичного трехчлена и определить знак одного из интервалов(потом чередуются)
10. Объясните графический решения квадратных неравенств.
11. Как решаются системы неравенств с одной переменной?
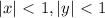
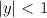возвести в квадрат, получив, 
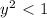, что и требовалось проверить.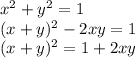
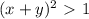
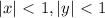, следует, что 0 <x < 1, 0 < y < 1
y`(x)=15*(2x-5)¹⁴*(2x-5)`=15*2*(2x-5)¹⁴=30(2x-5)¹⁴