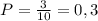
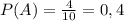
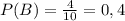
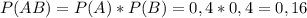
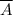 и найдём его вероятность.
и найдём его вероятность.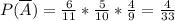
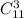 ). И вычислить число вариантов выбора 3 нарциссов из 6 (
). И вычислить число вариантов выбора 3 нарциссов из 6 ( ). А потом по классической формуле вероятности находится требуемая вероятность. Не всегда, но в данном случае такой путь боле громоздок.
). А потом по классической формуле вероятности находится требуемая вероятность. Не всегда, но в данном случае такой путь боле громоздок.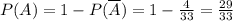
1. а) Х⁸+Х⁴-2=(Х⁴+2)*(Х⁴-1)=(Х⁴+2)*(Х²+1)*(Х²-1)=(Х⁴+2)*(Х²+1)*(Х+1)*(Х-1)
б) А⁵-А²-А-1=(А⁵-А)-(А²+1)=А*(А²-1)*(А²+1)-(А²+1)=(А²+1)*(А³-А-1)
2. А²-1=(А-1)*(А+1)
Из трех последовательных чисел одно делится на 3. Поскольку А на 3 не делится, то делится либо А-1, либо А+1.
3. Если домножить на 1, точнее на 2 - 1, то получил последовательность разностей квадратов, в результате чего получаем 2⁶⁴-1.
4. Поскольку 3 * Х делится на 3, 7 при делении на 3 дает в остатке 1, а 23 дает в остатке 2, то Y = 2 , следовательно, Х = 3
m-(n+m-p)=m-n-m+p=-n+p=p-n
3(x-y)+3y=3x-3y+3y=3x
3(a-b)-3a=3a-3b-3a=-3b
8(a-b)+8b=8a-8b+8b=8a
2(a+b)-2a=2a+2b-2a=2b
-3(x+y)-2(x-y)=-3x-3y-2x+2y=-5x-y