Первый признак подобия треугольников.
Если угол одного треугольника равен углу другого, а стороны, образующие этот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.
Второй признак подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Третий признак подобия треугольников.
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то такие треугольники подобны.
А если тебя интересует равенство треугольников, смотри сюда:
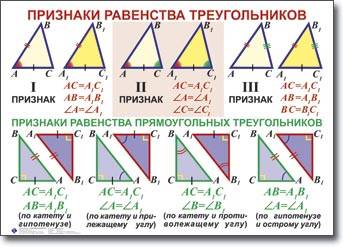
1 этап составление модели.
2 этап работа с моделью
3 этап ответ
составление модели: пусть а см - одна сторона прямоугольника, b см - другая сторона. периметр будет равен 2(a+b) см. по условию периметр равен 50. значит 2(a+b)=50
При увеличении стороны в 3 раза, то есть 3a см, а другой стороны уменьшив на 7см, то есть (b-7) см, получим периметр 2(a+(b-7)) см, по условию он равен 84 см. получим второе уравнение 2(a+(b-7))=84
решив систему из двух уравнений
2 этап
2(a+b)=50
2(3a+(b-7))=84
выразим из первого уравнения b=50:2-a
b= 25-a
подставим значение b во второе уравнение
2(3a+(25-a))=84
раскроем скобки и решим
получим 3a-a=42+7-25
a=12. b=13
ответ.
Одна сторона прямоугольн ка равна 12 см, другая 13 см
Cкорость II поезда V2= у км/ч.
Первая часть задачи:
Скорость сближения поездов Vсбл.= (х+у) км/ч
Время в пути до момента встречи t1= 6 часов
Расстояние S= 6(х+у) = 840 км
Вторая часть задачи:
Время в пути I поезд = 1,75 +5 = 6,75 ч.
Расстояние ( I поезд) S1= 6.75х км
Расстояние ( II поезд ) S2= 5y км
S= S1 + S2 = 6.75x +5y = 840 км
Система уравнений:
{6(x+y) = 840 |:6
{6.75x +5y = 840 | : (-5)
{x+y = 140 ⇒у=140-х
{- 1.35x - y = -168
Метод сложения:
х+у+ ( - 1,35х -у) = 140 + (-168)
х - 1,35х = -28
х(1 - 1,35) = -28
-0,35х=-28
х= (-28)/(-0,35)
х= 80 (км/ч) V1
у= 140 - 80 = 60 (км/ч) V2
ответ : 80 км/ч скорость I поезда, 60 км/ч скорость II поезда.