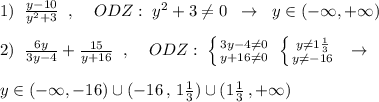
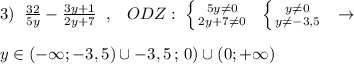
Наречия на -о (-е), образованные от качественных имен прилагательных, имеют две степени сравнения: сравнительную и превосходную.
Сравнительная степень наречий имеет две формы и составную форма сравнительной степени образуется с суффиксов -ее (-ей), -е, -ше от исходной формы наречий, от которой отбрасываются конечные -о (-е), -ко.
Составная форма сравнительной степени наречий образуется путем сочетания наречий и слов более и менее.
Превосходная степень наречий имеет, как правило, составную форму, которая представляет собой сочетание двух слов — сравнительной степени наречия и местоимения всех (всего).
1) х ∈ (7/5; ∞)
2) х ∈ (-1; 0)
3) х ∈ [-0,6; 2]
Объяснение:
1) Находим нули функции:
(5 х−7 ) = 0; х 1 = 7/5;
х^2−4х+5 = 0 - дискриминант отрицательный, значит уравнение не имеет действительных корней, то есть график данной функции с осью х не пересекается, а т.к. ветви параболы направлены вверх, то фунция положительна при любом значении х.
Определим знак (5 х−7) правее точки 7/5; например, возьмём точку х=2, получаем 10-7 = +3, знак + говорит о том, что функция положительна.
Объединяя 2 полученных значения, получаем ответ:
х ∈ (7/5; ∞) .
ответ: х ∈ (7/5; ∞).
2) Находим нули функции, приравнивая каждую скобку 0 и решая уравнения:
выражение в первых скобках даёт 2 корня: х1 = 0, х2 = 3;
выражение во второй скобке даёт один корень: х = -1;
выражение в третьей скобке даёт один корень: х =3.
Наносим на числовую ось все полученные корни:
-1, 0, 3.
Определим знак функции на участке от 0 до 3; пусть х = 1, тогда значение выражения:
(3-9)*(5+5)*(7-21) = (-6)*10*(-14) =+840 - знак + говорит о том, что участок от 0 до 3 нам не подходит;
возьмём точку правее 3, например, х = 5:
(3*25-45)*(25+5)*(35-21) = 30*30*14= +12600 - знак +, следовательно, значения х свыше 3 также не подходят;
диапазон от -1 до 0: возьмём точку -0,5:
(3*0,25+4,5)*(-2,5+5)*(-3,5-21) = 5,25* 2,5* (-24,5) = - 321,5625 - знак "-", следовательно, диапазон значений от -1 до 0 нас устраивает, так как на этом участке заданная функция отрицательна;
проверим последний участок (левее точки -1), возьмём точку х = -5:
(3*25+45)*(-25+5)*(-35-21) = 120*(-20)*(-56) = +134400 - знак +, следовательно, значения х меньше (-1) нас не устраивают.
ответ: х ∈ (-1; 0).
3) ( x−2 )(5 x+3)2≤0
Раскроем скобки:
10х² -14х -12=0
Находим нули функции:
х1= 2,
х2= - 3/5 = - 0,6
Ветви параболы направлены вверх, следовательно, решением будут все значения от -0,6 до 2 включительно, т.к., согласно условию, "и равно".
Тем не менее, проверим знак функции на участке от -0,6 до 2.
Пусть х = 0, тогда:
( x−2 )(5 x+3)2 = (-2)* 3* 2 = -12, - знак "-" говорит о том, что функция на этом участке отрицательна, что подтверждает правильность сделанного нами вывода.
ответ: х ∈ [-0,6; 2].