Масса второго сплава составляет 30 кг
Объяснение:
Для удобства вычислений переведём проценты в десятичные дроби:
5%=5:100=0,05
14%=14:100=0,14
10%=10:100=0,1
Пусть масса первого сплава равна х кг,
тогда масса второго сплава равна (х+6) кг,
а масса третьего сплава равна х+х+6=2х+6 кг
Масса цинка в первом сплаве составляет 0,05х кг,
масса цинка во втором сплаве составляет 0,14(х+6) кг,
масса цинка в третьем сплаве составляет 0,1(2х+6) кг.
Т.к. третий сплав состоит из первого и второго, составляем уравнение:
0,05х+0,14(х+6)=0,1(2х+6)
0,05х+0,14х+0,84=0,2х+0,6
0,84-0,6=0,2х-0,05х-0,14х
0,24=0,01х
х=0,24:0,01
х=24 (кг) - масса первого сплава
х+6=24+6=30(кг) - масса второго сплава
пояснения прилагаю.
1) 1.
⅓ =
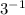
отсюда: - 1 × (x + 1) = - x - 1
2. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
2) 1. выносим общий множитель за скобку, используя одно из свойств показательных выражений:
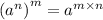
2. делим выражение на коэффициент при x
3. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
3) 1. преобразовав выражение (от перемены мест множителей проивзедение не меняется),
можно сделать замену, приводящую уравнение к квадратному.
первый корень: x ∉ R, так как значения показательной функции всегда положительны (иными словами, если строить график, то ни x, ни y никогда не будут принимать отрицательные значения).

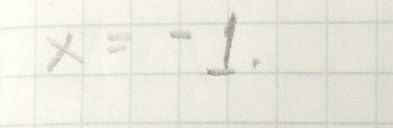
Находим массу соли в каждом растворе. Легче по пропорции.
100г100% раствора
хг20% соли х1 = 20г в первом растворе
300 г 100% р-ра
хг.10% соли х2=30г соли во втором растворе
общая масса соли равна: 20+30=50 г
общая масса полученного раствора : 100+300=400г.
400г100%
50гх% х=12,5%
ответ: 12,5%