№1
х2+5х-6=0
2x +5x - 6 = 0
7x - 6 = 0
7x = 6
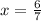
№2
Зх2+2х-1=0
6x+2x - 1=0
8x -1 = 0
8x=1
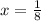
№3
х2-8х-84=0
2x-8x-84 =0
-6x - 84 = 0
-6x = 84
x = -14
№4
х2-5х+6=0
2x - 5x +6 =0
-3x+6 =0
-3x = -6
x= 2
№5
х2+4х+4=0
2x + 4x +4 = 0
6x +4 =0
6x = -4
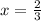
№6
2х2+3х+1=0
4x+3x+1 =0
7x+1 =0
7x = -1
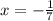
№7
4х2+10х-6=0
8x+10-6 =0
18x -6 =0
18x=6
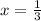
№8
3х2+32х+80=0
6x +32x +80 = 0
38x +80 =0
38x = -80
x = - 40/ 19
№9
х2=2х-48
2x = 2x - 48
0 = - 48
(утверждение ложно )
№10
–х2=5х-14
-2х = 5х - 14
-2х -5х = - 14
-7х = -14
х = 2
№11
х2+7х+2=0
2х+7х +2 = 0
9х +2 = 0
9х = -2
х = -2/9
№12
16х2-9=0
32х -9 = 0
32х = 9
х= 9/32
№13
–х2+х=0
-2х +х = 0
-х = 0
х = 0
№14
3х2-12х=0
6х-12х=0
-6х=0
х = 0
№15
х2+2х=0
2х+2х =0
4х =0
х=0
№16
-2х2+14=0
-4х+14=0
-4х= - 14
х= 7/2
№17
6х2=0
12х =0
х=0
№18
х2-64=0
2х-64=0
2х = 64
х= 32
№19
6х(2х+1)=5х+1
12х'2 +6х = 5х+1
12х'2 +6х -5х -1 = 0
12х'2+х -1 =0
12х'2 +4х -3х - 1 =0
4х (3х+1) - (3х+1) = 0
(3х+1) (4х - 1) =0
3х + 1 =0
4х-1 = 0
х = - 1/3
х= 1/4
№20
(х-2)2=3х-8
2х-4 = 3х - 8
2х - 3х = -8 +4
-х = -4
х= 4
буду благодарна, если ты нажмёшь на » и оценишь ответ как «лучший ». удачи ❤️
(1-√2)² = 1 + 2 - 2*1*√2 = 3 - 2√2 ≈ 3 - 2*1,41 = 3 - 2,82 = 0,18 ∈ [0; 0,5)
ответ: Б).
Если не верите, то вот более строгое доказательство:
Предположим, вариант Б) верный. Тогда (1-√2)² должно быть меньше, чем 0,5, а также больше либо равно, чем 0. Проверим оба эти условия. Итак, сравним (1-√2)² и 0. Т.к. √2 > 1 (т.к. (√2)² = 2 > 1 = 1²), то число 1 - √2 точно не равно нулю, а значит, его квадрат точно больше нуля. Доказали. Теперь осталось доказать, что (1-√2)² меньше, чем 0,5, или что 3 - 2√2 меньше, чем 0,5, то есть:
3 - 2√2 < 0.5 ?
-2√2 < 0.5 - 3 ?
-2√2 < -2.5 ?
2√2 > 2.5 ?
√2 > 1.25 ?
Т.к. (√2)² = 2 > 1.5625 = (1,25)², то и √2 > 1.25, а значит исходное выражение ((1-√2)² < 0.5) - верное, а значит, наше предположение, что ответ Б) - верный, оказалось правильным. Да, действительно (1-√2)² ∈ [0; 0,5)
г)b-(4-2b)+(3b-1)=b-4+2b+3b-1=6b-5
Я думаю, что так.Надеюсь, что з