Для начала поймём, что от нас хотят: нам говорят дискриминант и обычное линейное уравнение в данном случае. Решим дискриминант, а после начертим полученные точки на координатной плоскости и получим линию(и):
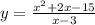
Дискриминант:
x²+2x-15=0
a=1 b=2 c=-15
D = 2²-4*1*(-15) = 4+60 = √64 > 0, возможно два корня.
Для удобства сразу превратим корень в обычное число:(необязательно, можно посчитать и в уме)
√64 = 8, подробнее в таблице чисел от 1 до 10.
x = 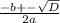
x₁ = 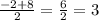
x₂ = 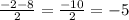
Заменяем и пишем вместо дискриминанта полученные его корни уравнения:
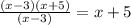
То есть единственный, оставшийся график линейной функции:
y = x+5
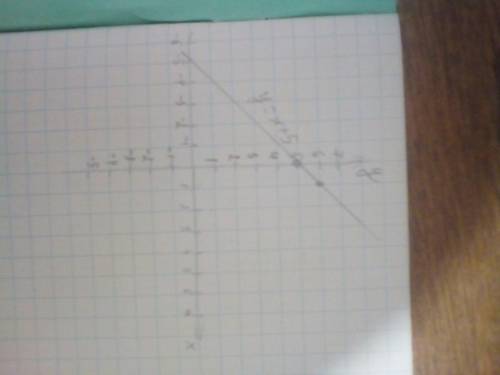
Построим таблицу:
x | 0 1
y | 5 6
Всё просто: подставляем вместо x число и получаем число для значения y:
y₁ = 0+5 = 5
y₂ = 1+5 = 6
Теперь строим график по точкам и готово! Фотография графика:
а) Во-первых, если с =0, то уравнение превратится в линейное -5х+2=0, корень его 0,4.
Во-вторых, если два одинаковых корня назвать одним, то будет у уравнения единственный корень, когда дискриминатнт равен нулю, т.е.
когда 25-16с=0, т.е., когда с =25/16=1,5625
б) Если с=6, то пропадает икс в квадрате и получается линейное, 2х+2=0, откуда корень минус единице равен.
Если же первый коэффициетн отличен от шести, то тогда единственный корень будет, когда дискриминант равен нулю, а именно, когда
(с-4)²-4*(с-6)*2=0
с²-8с+16-8(с-6)=с²-8с+16-8с+48=с²-16с+64=(с-8)²=0,когда
с=8
Действительно, тогда уравнение примет вид 2с²-4с+2=0
с²-2сс+1=0
(с-1)²=0, единственный корень с=1, правда двукратный.