При каких значениях a уравнение 2x^2+6x+a=0 не имеет корней?

Question

Алгебра: При каких значениях a уравнение 2x^2+6x+a=0 не имеет корней?

АУЕшник2281337 · Accepted Answer

Нахождение промежутков возрастания функции сводится к задаче нахождения таких значений Х, при которых производная от исходной функции будет больше 0.

Значит нам надо взять производную:

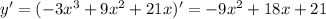
y'=(-3x^3+9x^2+21x)'=-9x^2+18x+21

Теперь осталось решить неравенство:

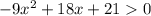
-9x^2+18x+210

найдем сначала корни уравнения:

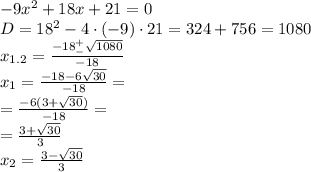
$-9x^2+18x+21=0 \\ D=18^2-4\cdot (-9) \cdot 21=324+756=1080 \\ x_{1.2}=\frac{-18 ^+_- \sqrt{1080}}{-18} \\ x_1=\frac{-18-6\sqrt{30}}{-18}= \\ =\frac{-6(3+\sqrt{30})}{-18}= \\ =\frac{3+\sqrt{30}}{3} \\ x_2=\frac{3-\sqrt{30}}{3}$

Это была парабола ветви которой направлены вниз, потому что перед 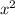x^2 стиот отрицательный коэффициент. Значит промежуток где 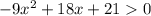-9x^2+18x+210 лежит между ее корней, значит и промежуток возрастания исходной функции лежит между ее корней.

Таким образом: функция возрастает на интервале: 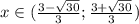$x \in (\frac{3-\sqrt{30}}{3};\frac{3+\sqrt{30}}{3})$

ответ: функция возрастает на интервале: 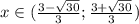$x \in (\frac{3-\sqrt{30}}{3};\frac{3+\sqrt{30}}{3})$

MOGZ ответил