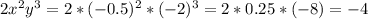
1) Пооскольку по условию AM = MB(из того, что CM-медиана), а AH = HC = 2, то MH-средняя линия ΔABC. MH = 0.5BC.
2)Рассмотрим ΔABH,<H=90°. AB = 3*2 = 6 - по свойству медианы. AH = 2. По теореме Пифагора, BH = √6² - 2² = √32 = 4√2.
3)рассмотрю ΔHBC,<H = 90°. По теореме Пифагора, BC = √(4√2)² + 4 = √36 = 6.
HM = 0.5 * 6 = 3.
Либо можно было решить чуть проще. Рассмотрим ΔABH,<H = 90°. Мы видим, что раз MH - средняя линия, то AM = MB. Следовательно, в ΔABH HM - медиана. Воспользуюсь особым свойством медианы, проведённо в прямоугольном треугольнике к гипотенузе: она равна половине гипотенузы. Значит, HM = 0.5 * AB = 3. Так решалась эта задача ))
Так как не написано, как именно измениться увеличится на 8 или уменьшится на 8. То разберём 2 случая.
1) Составим систему уравнений для первого случая из трёх взаимо-связанных уравнений:1) x+y=11
2) x^2+y^2=z
3) (x+4)^2+(y-4)^2=z+8
Подставим z из 2-ого уравнения в 3-ье
(x+4)^2+(y-4)^2=x^2+y^2+8
x^2+8x+16+y^2-8y+16=x^2+y^2+8
x^2 и y^2 взаимно уничтожаются
8x-8y+32=8
8x-8y=8-32
8(x-y)=-24
Рассмотрим 1-ое уравнение
x+y=11
Решим относительно x
x=11-y
Вернемся к уравнению 8(x-y)=-24 и вместо x подставим (11-y)
8((11-y)-y)=-24
8(11-2y)=-24
Обе части уравнения делим на 8
11-2y=-3
-2y=-3-11
-2y=-14
y=7
Подставим вместо y число 7 в 1-ое уравнение и найдём x
x=11-7=4
2) Составим систему уравнений для второго случая из трёх взаимо-связанных уравнений:1) x+y=11
2) x^2+y^2=z
3) (x+4)^2+(y-4)^2=z-8
Подставим z из 2-ого уравнения в 3-ье
(x+4)^2+(y-4)^2=x^2+y^2-8
x^2+8x+16+y^2-8y+16=x^2+y^2-8
x^2 и y^2 взаимно уничтожаются
8x-8y+32=-8
8x-8y=-8-32
8(x-y)=-40
Рассмотрим 1-ое уравнение
x+y=11
Решим относительно x
x=11-y
Вернемся к уравнению 8(x-y)=-40 и вместо x подставим (11-y)
8((11-y)-y)=-40
8(11-2y)=-40
Обе части уравнения делим на 8
11-2y=-5
-2y=-5-11
-2y=-16
y=8
Подставим вместо y число 8 в 1-ое уравнение и найдём x
x=11-8=3
Следовательно в первом случае это число 47, а во втором 38.ответ: 47, так как таких чисел несколько, а в ответ нужно написать большее.Объяснение: