

Подобные выражения приводятся к квадрату стоящему под основным корнем.
например, в данном случае 3 = 2 + 1, где 2 - это квадрат √2, а 1 - это квадрат 1, таким образом, под корнем получается
√(2 - 2√2 + 1) = √((√2)² - 2·1·√2 + 1) = √(√2 - 1)²
Почему мы сгруппировали так: √((√2)² - 2·1·√2 + 1) = √(√2 - 1)² , а не так:
√((√2)² - 2·1·√2 + 1) = √(1 - √2)²?
Потому что при извлечении квадратного корня должно получиться положительное число, т.к. по определению
"Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а"
√2 ≈1,41 > 1, поэтому √2 - 1 > 0
Итак,
(√2)² - 2·1·√2 + 1) = √(√2 - 1 )² = √2 - 1
Довольно интересная задача, которая наверняка имеет множество решений, постараюсь поподробнее изложить своё.
Итак, возраст отца определяется двузначным числом a1a0, где a1 и a0 - цифры данного числа.
Представим данное число в виде разложения на слагаемые, по формуле перевода чисел в десятичную систему счисления:
a1a0 = a0 * 10^0 + a1 * 10^1 = a0 + 10a1.
Суммарный возраст отца и сына равен 67, запишем это в виде уравнения с двумя неизвестными:
a0 + a1 + a0 + 10a1 = 67
2a0 + 11a1 = 67, мы получили диофантово уравнение, которое требуется решить в натуральных числах, так как возраст - величина положительная.
Решим с использованием следующей системы неравенств:
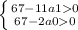
Решая получаем, что a1 < 6, а a0 < 33.
Интервал значений a0 слишком велик, поэтому будет отталкиваться от значений a1.
Теперь дело остаётся за банальным перебором:
Если a1 = 1, то возраст отца равен 128, что невозможно.
Если a1 = 2, то уравнение 2a0 + 11a1 = 67 в решении не нуждается, так как при подстановке получим, что сумма чётных чисел равна числу нечётному, что невозможно. Впредь будем рассматривать только те значения a1, которые не кратны двум.
Если a1 = 3, то возраст отца равен 317, что невозможно.
Значение 4 кратно 2, а значит заранее не подходит.
В итоге мы пришли к единственному оставшемуся значению - это 5, оно и будет решением данного уравнения, проверим это.
2a0 + 55 = 67
2a0 = 12
a0 = 6
Возраст отца равен 56, тогда возраст сына - 11.
Искомый ответ: 11.