№1 (а)
ответ: -\frac{4}{3}" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=x%20%3E%20-%5Cfrac%7B4%7D%7B3%7D" title="x > -\frac{4}{3}">
№1 (б)
№2 (а)
-4} \atop {x\leq -2.5}} \right." class="latex-formula" id="TexFormula6" src="https://tex.z-dn.net/?f=%5Cleft%20%5C%7B%20%7B%7Bx%3E-4%7D%20%5Catop%20%7Bx%5Cleq%20-2.5%7D%7D%20%5Cright." title="\left \{ {{x>-4} \atop {x\leq -2.5}} \right.">
№2(б)
\frac{36}{5}" class="latex-formula" id="TexFormula10" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
ответ: \frac{36}{5}" class="latex-formula" id="TexFormula12" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
1) Пусть последовательность положительных чисел
... ; 
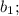
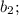
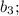
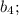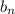
является геометрической прогрессией, тогда
с формулы общего члена геометрической прогрессии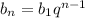 
данную последовательность представим в виде:
... ; 
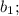
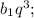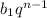
2) Прологарифмируем по основанию 
:
... ; 
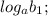
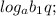
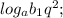
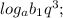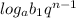
3) Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
. . . . . . . . . . . . . . . . . . . . . . . .
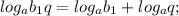
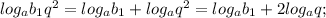
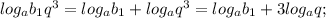
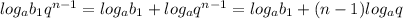
4) Рассмотрим полученную последовательность:
... ; 
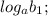
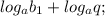
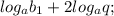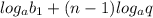
Очевидно, это арифметическая прогрессия, где
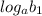- её первый член
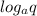- разность этой прогрессии.
Доказано.
решение прикреплено
Объяснение: