22. -2
23. 1
Объяснение:
22. Рассмотрим каждое из подкоренных выражений:

Поскольку квадрат какого-либо числа неотрицателен, 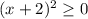 , отсюда:
, отсюда:

Значит, левая часть ![\sqrt[3]{2x^2+8x+72}+\sqrt[3]{3x^2+12x+12}\geq \sqrt[3]{64}+\sqrt[3]{0}=4](/tpl/images/4540/3998/87f22.png)
Правая часть 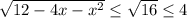
Левая часть не меньше 4, а правая не больше 4. Значит, равенство достигается тогда и только тогда, когда обе части равны 4. Правая часть равна 4:
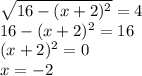
Проверим этот корень для левой части:
![\sqrt[3]{2(-2+2)^2+64}+\sqrt[3]{3(-2+2)^2}=\sqrt[3]{64}+\sqrt[3]{0}=4](/tpl/images/4540/3998/4cb78.png) — верно.
— верно.
Уравнение имеет единственный корень x = -2.
23. Заметим, что 
Значит, 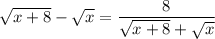 (знаменатель не обращается в ноль, так как x ≥ 0 по ОДЗ, значит,
(знаменатель не обращается в ноль, так как x ≥ 0 по ОДЗ, значит, 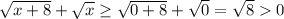 ).
).
Пусть  . Тогда уравнение имеет вид:
. Тогда уравнение имеет вид:
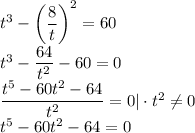
Заметим, что t = 4 — корень многочлена левой части. Поделив его столбиком на (t - 4), получим его разложение на множители:

Поскольку t > 0,  , значит, обе части можно поделить на второй множитель, так как он не равен нулю. Получаем:
, значит, обе части можно поделить на второй множитель, так как он не равен нулю. Получаем:

Левая часть неотрицательна, значит, правая часть также неотрицательна: 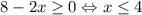
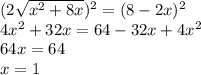
Корень удовлетворяет условиям 0 ≤ x ≤ 4, значит, он подходит.
Производная функции:
x^2 -4x +3
Определим критические точки:
x^2 -4x + 3 = 0
D/4 = 4 -3 = 1
x1 = 2 + 1 = 3, x2 = 2 -1 = 1
Имеем 3 интервала:
1) -беск; 1
2) 1;3
3) 3;беск
Найдем интервалы монотонности, определив знак 1 производной:
1) +
2) -
3) +
График производной - парабола исходящая из точки (2;-1)