8
Объяснение:
Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то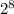 
сравнимо с 1 по модулю 15.
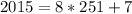
Тогда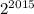 
можно записать в виде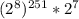 
Поскольку мы выяснили, что 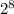сравнимо с 1 по модулю 15, то 
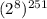также сравнимо с 1 по модулю 15.
Остаётся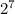 
, которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
То есть можем записать: 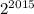≡ ≡ 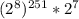≡ 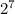8 mod 15
Это значит, что остаток равен 8.
N(2) - сколько чисел без 2; N(3) - сколько чисел без 3; N(2#3) - сколько чисел и без 2, и без 3; N - общее количество пятизначных чисел. Чтобы получить ответ в задаче, нужно из N вычесть N(2) и N(3), но при этом учесть, что в результате мы дважды уберем из подсчета числа, в которые не входят ни 2, ни 3. Поэтому к ответу нужно добавить еще N(2#3).
Итак, ответом к задаче будет
N-N(2)-N(3)+N(2#3)=9·10·10·10·10-8·9·9·9·9-8·9·9·9·9+7·8·8·8·8=13696.
Все подсчеты производились одним и тем же , Например, при подсчете N (хотя ответ многие знают и без вычислений) мы рассуждаем так: на первое место претендует любая цифра, кроме нуля (9 претендентов) - ведь первая цифра не может быть нулем, на каждое следующее - любая из 10 цифр. остается перемножить 9 и четыре десятки. N(2) вычисляется аналогично, только теперь на первое место 8 претендентов, а на остальные по 9. Ну и так далее.
ответ: 13696
S₂₅=(a₁+a₂₅)*25/2
(a₁+a₂₅)*25/2=300
a₁+a₂₅=24
a₁+a₁+24d=24
2a₁+24d=24 |:2
a₁+12d=12
a₁₃=a₁+12d => a₁₃=12