Объяснение:
До расширения было х рядов по у деревьев в каждом, всего 180 деревьев:
х*у=180
После расширения стало (х+5) по (у+3) деревьев в каждом, всего стало 180+120=300 деревьев
(х+5)*(у+3)=300
Получаем систему уравнений:
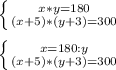
подставим значение х во второе уравнение
(180/у+5)*(у+3)=300
(180+5у)/у *( у+3)=300
(180+5у)*(у+3)=300у
180у+540+5у²+15у-300у=0
5у²-105у+540=0
разделим на 5
у²-21у+108=0
у₁,₂=(21±√21²-4*108)/2=(21±√441-432)/2=(21±√9)/2
у₁=(21+3)/2=12 деревьев , х₁=180:12=15 рядов
у₂=( 21-3)/2=9 деревьев , х₂= 180 : 8=20 рядов
Получаем , что размещение деревьев имеет два варианта
Вариант №1
15 рядов по 12 деревьев в одном ряду
Вариант №2
20 рядов по 9 деревьев в каждом ряду
1) 1-sin²a = cos²a sin²a+cos²a. по основному тригонометрическому тождеству
следовательно √(1-sin²a)=√cos²a =| cos(a) | (по модулю)
поскольку в данном интервале cos(a) положительный => модуль можно убрать.
ответ: cos(a)
2) ctg(a) = cos(a)/sin(a)
1 + ctg²(a) = 1 + cos²(a)/sin²(a) = (sin²a+cos²a)/sin²a = 1/sin²a (sin²a+cos²a =1
по основному тригонометрическому тождеству)
√1+ctg²a = √(1/sin²a) = | 1/sin(a) |
так как на данном промежутке sin(a) отрицательный => | 1/sin(a) | = - 1/sin(a)
ответ: -1/sin(a).
Заменим сумму косинусов по формуле "удвоенное произведение косинуса полусуммы на косинус полуразности":
2cos^2 x+2cos 4x·cos 2x=0;
Теперь заменим первое слагаемое по формуле понижения степени у косинуса на 1 плюс косинус двойного угла, а cos 4x по формуле косинус двойного угла:
1+cos 2x+2(2cos^2 2x-1)·cos 2x=0;
cos 2x=t;
1+t+4t^3-2t=0;
4t^3-t+1=0; умножим уравнение на 2 и сделаем замену 2t=q:
q^3-q+2=0.
Поскольку рациональные корни не угадываются, можно попробовать решить с формул Кардано. Чтобы узнать, что из этого получается, смотри дальнейшие выкладки. Мне кажется, они говорят о том, что в условие вкралась ошибка
q=p+(1/(3p)); тогда q^3=p^3+(1/(27p^3)) +3p^2(1/(3p))+3p(1/(9p^2); подставив в уравнение, получаем
p^3+(1/(27p^3))+2=0; домножаем на 27p^3 и заменяем p^3 на r:
27r^2+54r+1=0; для упрощения вычислений еще одна замена (перед ней умножаем уравнение на 3) 9r=z;
z^2+18z+3=0; z=- 9+-√78; r=-1+-√78/9;
p=∛(-1+-√78/9);
q= ∛(-1+-√78/9)+1/(3∛(-1+-√78/9));
cos 2x = t= (∛(-1+-√78/9)+1/(3∛(-1+-√78/9)) /2
До ответа доводить не хочется, лучше если сначала автор задачи перепроверит условие. По любому мои скромные попытки кому-то могут показаться любопытными.