Алгебра: 5b^2-14ab/25b^2-196a^2 при a=-корень из 2 ,b=корень из 8

5b^2-14ab/25b^2-196a^2 при a=-корень из 2 ,b=корень из 8

👇

Ответ:

madamburkova20

15.02.2023

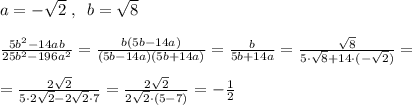
$a=-\sqrt2\; ,\; \; b=\sqrt8\\\\ \frac{5b^2-14ab}{25b^2-196a^2} = \frac{b(5b-14a)}{(5b-14a)(5b+14a)} = \frac{b}{5b+14a} = \frac{\sqrt8}{5\cdot \sqrt8+14\cdot (-\sqrt2)} =\\\\= \frac{2\sqrt2}{5\cdot 2\sqrt2-2\sqrt2\cdot 7} = \frac{2\sqrt2}{2\sqrt2\cdot (5-7)} =-\frac{1}{2}$

4,8(71 оценок)

Открыть все ответы

Ответ:

KaraKiller

15.02.2023

Нам дан прямоугольный треугольник. Вспомним, как можно найти его площадь:

S = 1/2 a*b, где a и b -- катеты треугольника.

Также вспомним теорему Пифагора: C² = A² + B², где С -- гипотенуза, а А и В -- катеты.

Пусть А -- меньший катет, который равен х. Тогда гипотенуза будет равна (х + 9). Чтобы найти второй катет, выразим его из теоремы Пифагора:

В² = С² - А²

Теперь подставим значения:

В² = (x + 9)² - x²

Мы видим формулу разности квадратов, раскроем её:

В² = (x + 9 - x)(x + 9 + x) = 9(2x + 9)

Тогда В = 3√(2х + 9).

Подставим полученные выражения в формулу площади:

S = 1/2 * a * b = 1/2 * x * 3√(2x + 9); S = 60 =>

60 = 1/2x * 3√(2x +9)

120 = 3x√(2x + 9)

x√(2x +9) = 40

Возведём всё в квадрат, чтобы избавиться от корня:

x² * (2x + 9) = 1600

Перемножим:

2x³ + 9x² - 1600 = 0

Чтобы разложить на множители представим 9х как (25х - 16х):

2x³ - 16x² + 25x² - 1600 = 0

Сгруппируем попарно и вынесем общий множитель из каждой пары:

(2x³ - 16x²) + (25x² - 1600) = 0

2x² (x - 8) + 25 (x² - 64) = 0

Разложим разность квадратов во второй скобке:

2x² (x - 8) + 25 (x - 8)(x + 8) = 0

Вынесем общий множитель (х - 8) за скобку:

(x - 8) (2x² + 25 (x + 8) = 0

Раскроем третью скобку:

(x - 8) (2x² + 25x + 200) = 0

x - 8 = 0 или 2x² + 25x + 200 = 0

Рассмотрим оба случая:

1. x - 8 = 0

x = 8

2. 2x² + 25x + 200 = 0

D = b² - 4ac = 625 - 4*400 = 625 - 1600.

Дискриминант отрицательный, значит в данном уравнении корней нет.

Итак меньший катет равен 8, тогда гипотенуза равна:

8 + 9 = 17

А второй катет, или катет В:

3√(2х + 9) = 3√(2*8 + 9) = 3√ (16 + 9) = 3√25 = 3*5 = 15.

ответ: Меньший катет равен 8, гипотенуза равна 17, больший катет равен 15.

4,8(20 оценок)

Ответ:

Danil200000006

15.02.2023

Рассмотрим сначала числа со старшим разрядом единиц
(в обратном порядке):

$9^2 = 81 \ ;$        сумма количества цифр: 1 + 2 = 3 , количество цифр у квадрата числа вдвое больше количества цифр исходного числа.

$4^2 = 16 \ ;$        искомая сумма: 1 + 2 = 3 , количество цифр у квадрата числа всё так же вдвое больше количества цифр исходного.

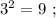$3^2 = 9 \ ;$        искомая сумма: 1 + 1 = 2 , количество цифр у квадрата равно количеству цифр исходного.

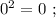$0^2 = 0 \ ;$        искомая сумма: 1 + 1 = 2 , количество у квадрата равно количеству цифр исходного.

Теперь переходим к старшему разряду десятков
(в обратном порядке):

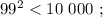$99^2 < 10 \ 000 \ ;$        сумма: 2 + 4 = 6 , количество цифр у квадрата вдвое больше количества цифр исходного.

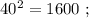$40^2 = 1600 \ ;$        сумма: 2 + 4 = 6 , цифр у квадрата всё так же вдвое больше количества цифр исходного.

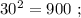$30^2 = 900 \ ;$        сумма: 2 + 3 = 5 , цифр у квадрата числа: 3 = 4–1 .

$10^2 = 100 \ ;$        сумма: 2 + 3 = 5 , цифр у квадрата: 3 = 4–1 .

Далее переходим к старшему разряду сотен
(в обратном порядке):

$999^2 < 1 \ 000 \ 000 \ ;$        сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.

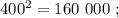$400^2 = 160 \ 000 \ ;$        сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.

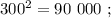$300^2 = 90 \ 000 \ ;$        сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .

$100^2 = 10 \ 000 \ ;$        сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .

Ну и ещё переходим к старшему разряду тысяч
(в обратном порядке):

$9 \ 999^2 < 100 \ 000 \ 000 \ ;$        сумма: 4 + 8 = 12 , у квадрата вдвое больше.

$4000^2 = 16 \ 000 000 \ ;$        сумма: 4 + 8 = 12 , у квадрата вдвое больше.

$3000^2 = 9 \ 000 000 \ ;$        сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .

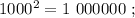$1000^2 = 1 \ 000 000 \ ;$        сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .

А теперь всё обобщим на самый общий случай.

Если бы число записывалось единицей с R нолями, то его квадрат содержал бы уже 2R нолей, при этом в исходном числе было бы (R+1) цифр, а в квадрате числа – (2R+1) цифр.

Пусть у нас старший разряд таков, что во всём числе только R цифр, рассмотрим всё, как обычно в обратном порядке:

( 99999 : : : R цифр : : : 99999 )   –   это число на единицу меньше, чем число     ( 100000 : : : R нулей : : : 00000 )     , в котором (R+1) цифр.

квадрат числа [( 99999 : : : R цифр : : : 99999 )]    –   это число, меньшее, чем число     ( 100000 : : : 2R нулей : : : 00000 )     , в котором (2R+1) цифр.

Значит, квадрат числа ( 99999 : : : R цифр : : : 99999 ) содержит ровно 2R цифр, а всего само число и его квадрат содержат 3R цифр.

в числе ( 400000 : : : (R–1) нулей : : : 00000 ) содержится R цифр.

квадрат числа [( 400000 : : : (R–1) нулей : : : 00000 )] =
= ( 1600000 : : : (2R–2) нулей : : : 00000 ) содержит 2R цифр, а всего само число и его квадрат содержат 3R цифр.

в числе ( 300000 : : : (R–1) нулей : : : 00000 ) содержится R цифр.

квадрат числа [( 300000 : : : (R–1) нулей : : : 00000 )] =
= ( 900000 : : : (2R–2) нулей : : : 00000 ) содержит (2R–1) цифр, а всего само число и его квадрат содержат (3R–1) цифр.

в числе ( 100000 : : : (R–1) нулей : : : 00000 ) содержится R цифр.

квадрат числа [( 100000 : : : (R–1) нулей : : : 00000 )] =
= ( 100000 : : : (2R–2) нулей : : : 00000 ) содержит (2R–1) цифр, а всего само число и его квадрат содержат (3R–1) цифр.

И так будет для любого R

R = 1   : : : сумма: 3R = 3 или (3R–1) = 2 .
R = 2   : : : сумма: 3R = 6 или (3R–1) = 5 .
R = 3   : : : сумма: 3R = 9 или (3R–1) = 8 .
R = 4   : : : сумма: 3R = 12 или (3R–1) = 11 .
R = 5   : : : сумма: 3R = 15 или (3R–1) = 14 .

. . .

R = 32   : : : сумма: 3R = 96 или (3R–1) = 95 .
R = 33   : : : сумма: 3R = 99 или (3R–1) = 98 .
R = 34   : : : сумма: 3R = 102 или (3R–1) = 101 .
R = 35   : : : сумма: 3R = 105 или (3R–1) = 104 .

... и т.д и т.п. ...

Как легко видеть, в этой последовательности:

2, 3, 5, 6, 8, 9, 11, 12, 14, 15 .... 95, 96, 98, 99, 101, 102, 104, 105 ....

пропущены определённые числа. Пропущенные числа:

1, 4, 7, 10, 13, 16 .... 94, 97, 100, 103, 106 ....

подчиняются закону (3R+1).

В самом деле, между предыдущим и последующим значениями, кратными трём, всегда содержатся два целые числа, а искомой суммой, помимо 3R, может быть только одно из них: (3R–1) .

Поэтому, значения, подчиняющиеся закону (3R+1) не могут быть искомым результатом. Так, например, число 99 – кратно трём ( 99 = 3*33 ), а значит, число   100 = 3*33+1   никак не могло бы оказаться в расчётах Лены.

О т в е т : у Лены не могли получиться результаты, подчиняющиеся закону (3R+1) , где R – какое угодно целое число.

ну и, конечно, все результаты Лены могут быть только положительными, поскольку это количества, т.е. натуральные величины.

в частности, у неё не могло получиться число 100.

4,4(48 оценок)

Это интересно:

Компьютеры-и-электроника

28.03.2021

Как удалить историю веб поиска в Google: простые шаги для защиты вашей конфиденциальности...

Дом-и-сад

27.10.2021

Как найти распределительный щиток или блок предохранителей...

Мир-работы

05.04.2023

Как пережить увольнение: советы профессионалов...

Дом-и-сад