Нужно найти первый член прогрессии,где b3=1/2 и b7= 1/32( прогрессия не отрицательна)

Question

Алгебра: Нужно найти первый член прогрессии,где b3=1/2 и b7= 1/32( прогрессия не отрицательна)

Начинайко · Accepted Answer

Пусть боковая сторона равнобедренного треугольника - х см, тогда основание треугольника будет 18-2х или 2(9-х) см.

Составим выражение для высоты треугольника, проведенной к основанию

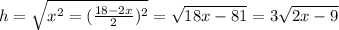
$h=\sqrt{x^2=(\frac{18-2x}{2})^2}=\sqrt{18x-81}=3\sqrt{2x-9}$

Теперь составим выражение площади треугольника

$S=\frac{1}{2}\cdot 3\sqrt{2x-9}\cdot 2(9-x)=3\sqrt{2x-9}\cdot (9-x)$

Найдем производную полученного выражения

$S'=\frac{3\cdot 2\cdot(9-x)}{2\sqrt{2x-9}}-3\sqrt{2x-9}=3\cdot \frac{9-x-2x+9}{\sqrt{2x-9}}=\\\ =9(\frac{6-x}{\sqrt{2x-9}}) \\\\ S'=0\\ 9(\frac{6-x}{\sqrt{2x-9}})=0\\\ 2x-9\neq0\\ x\neq4,5\\ 6-x=0\\ x=6\\$

при x<6 значение производной S'>0, а при x>6 S'<0, значит при х=6 функция S принимает максимальное значение (максимум функции)

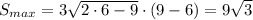
$S_{max}=3\sqrt{2\cdot 6-9}\cdot (9-6)=9\sqrt{3}$

Таким образом, плащадь треугольника будет наибольшей, если все его стороны будут равны 6 см, т.е. он будет равносторонним.

MOGZ ответил