Объяснение:
 ,
, 
данная функция квадратическая, ее график парабола состоит из двух ветвей с общей точкой - вершиной параболы, которые в общем случае делят ее на две подфункции, у каждой из которых своя своя обратная функция
так в базовом виде это для параболы 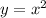 вершина (0;0) можно выделить две обратные функции
вершина (0;0) можно выделить две обратные функции  и
и ![y=\sqrt{-x}; D(y)=(-\infty; 0]](/tpl/images/1404/8602/70398.png)
для данной параболы 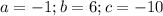
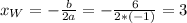
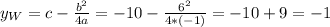
а значит имеем одну ветвь параболы
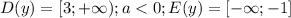
(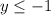 )
)
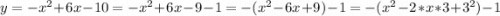
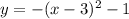
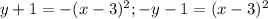
так как 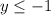 :
: 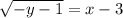
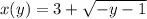 --- график тот же что и у исходной функции, но "обратная" зависимость переменных
--- график тот же что и у исходной функции, но "обратная" зависимость переменных
меняем обозначения (x,y)->(y,x) и получим что
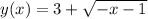 ,
, ![D(y)=[-\infty; -1]](/tpl/images/1404/8602/c649e.png) А это уравнение обратной функции, график симметричен исходной функции относительно прямой y=x
А это уравнение обратной функции, график симметричен исходной функции относительно прямой y=x
------------------------------------------------------------------------------------
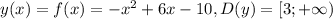
![y(x)=f^{-1} (x)=3+\sqrt{-x-1}, D(y)=[-\infty; -1]](/tpl/images/1404/8602/874e3.png)
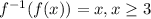
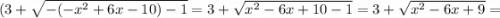
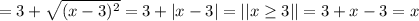
аналогично можно убедиться (помним только про области определения и действий функций), что
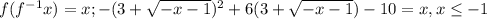
!! следует понимать что по факту есть две функции 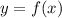 и
и 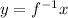 , x всего лишь условная буква, обозначающая независимый аргумент, y - условная буква, обозначающая значение функции - на их месте могли быть и другие буквы,
, x всего лишь условная буква, обозначающая независимый аргумент, y - условная буква, обозначающая значение функции - на их месте могли быть и другие буквы,
более важную роль для понимания обратных функций играет сами 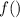 и
и 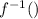 . (соблюдение взаимно однозначности), а х и y лишь для работы в системе координат XoY
. (соблюдение взаимно однозначности), а х и y лишь для работы в системе координат XoY
Найдем точку при x=−2
Заменим в выражении переменную x на −2
f(−2)=2(−2)−(−2)^3
Упростим результат.
f(−2)=−4−(−2)^3
Возведем −2 в степень 3
f(−2)=−4+8
f(−2)=−4+8
f(−2)=4
Итоговым ответом является 4
y=4
Найдем точку при x=−1
Заменим в выражении переменную x на −1
f(−1)=2(−1)−(−1)^3
Упростим результат.
f(−1)=−2+1
f(−1)=−1
Итоговым ответом является −1
y=−1
Найдем точку при x=0
Заменим в выражении переменную x на 0
f(0)=2(0)−(0)^3
f(0)=0−0^3
f(0)=0
Итоговым ответом является 0
y=0
Найдем точку при x=1
f(1)=2(1)−(1)^3
Упростим результат.
f(1)=2-1*1
f(1)=1
Итоговым ответом является 1
y=1
Найдем точку при x= 2
f(2)=2(2)−(2)^3
Упростим результат.
f(2)=−4−(2)^3
Возведем 3 в степень 3
f(2)=4-8
f(2)=-4
Итоговым ответом является -4
y=-4
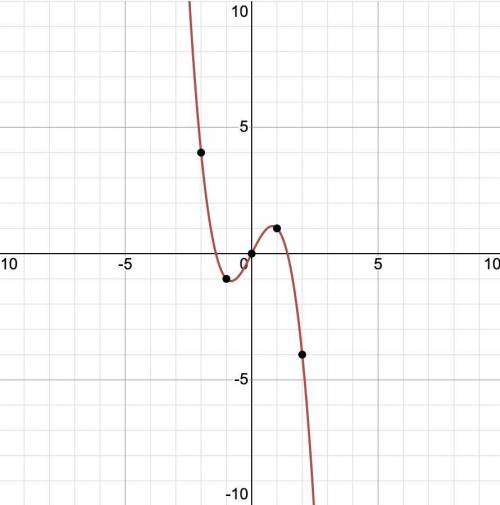
График кубической функции можно построить, учитывая поведение функции и используя данные точки.
x y
-2 4
-1 -1
0 0
1 1
2 -4
График кубической функции можно построить, учитывая поведение функции и используя выбранные точки. Возрастает влево и убывает вправо
x y
-2 4
-1 -1
0 0
1 1
2 -4