Дано:
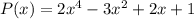
Найти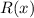 
- остаток от деления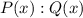 
Решение.
1) Для начала разложим многочлен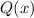 
на множители, для этого решим уравнение:
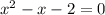
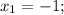
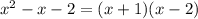
2) Так как данный многочлен 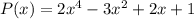делится на 
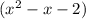с остатком, то представим его в виде
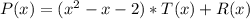
где
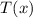- неполное частное;
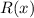- искомый остаток.
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
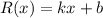
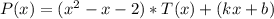
3) Подставим в равенство 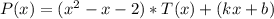первый корень 
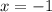и получим:
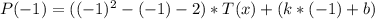
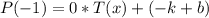
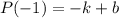
Вычислим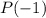 
.
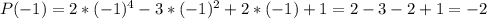
Так как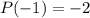 
, то
=> 
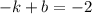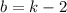
4) Аналогично решаем и со вторым корнем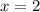 
.
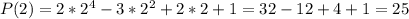
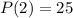
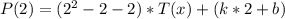
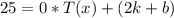
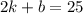
5) Подставим 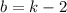в полученное уравнение:
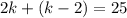
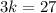
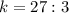
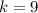
6) 
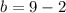
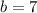
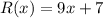- искомый остаток.
ответ: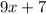 
k=2
в=3
Объяснение:
На рисунке график линейной
функции.
Линейная функция задается
уравнением:
у=kx+в
1.
k - угловой коэффициент.
k= tga
a - угол наклона графика
функции к положительному
направлению оси ОХ.
Из прямоугольного треу
гольника по определению
тангенса:
k=tgа=6/3=2
Отношение противолежащего
углу "а" катета к прилежащему
есть тангенс угла "а".
2.
Коэффициент "в" можно опре
делить, если в уравнении пря
мой принять х=0.
Если х=0, то:
у=kx+в=k×0+в=в
"в" - ордината точки пересече
ния графика линейной функ
ции с осью ОУ.
Коэффициент "в" показывает
смещение графика линейной
функции вдоль оси ординат
относительно точки начала от
счета.
Если в>0 график поднимается
вверх относительно точки(0; 0)
вдоль оси ОУ на "в" единиц.
Если в<0 график опускается
вниз относительно точки(0; 0)
вдоль осиОУ на "в" единиц.
(-2)^3 + 3*(-2)^2 - b*(-2) + 6 = 0;
-8 + 12 + 2b + 6 = 0;
10+2b = 0;
b = -10/2 = -5.