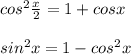
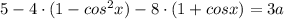
Получаем квадратное уравнение относительно
cosx=t
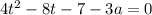
Это уравнение имеет хотя бы один корень, если D ≥0
D=64+16(7+3a)=16(11+3a)
D≥0⇒ 11+3a≥0⇒ a≥ -11/3
t₁=1- (√(11+3а))/2 или t₂=1+ (√(11+3а))/2
Обратная замена приводит к уравнениям вида cos=t₁ или cosx=t₂
Чтобы эти уравнения имели хотя бы один корень, необходимо, что бы
-1 ≤ t₁ ≤1 или -1 ≤ t₂ ≤1
Решаем неравенства:
-1 ≤1+ (√(11+3а))/2 ≤1
-2≤√(11+3а))/2≤0
-4≤√(11+3а)≤0
Решением неравенства является
11+3a=0
a=-11/3
t₁=t₂=1/2
cosx=1/2
x=±(π/3)+2πn, n∈Z
Неравенство
-1 ≤1- (√(11+3а))/2 ≤1
также приводит к ответу a=-11/3
О т в е т. При а=-11/3
x=±(π/3)+2πn, n∈Z
Бесконечная периодическая дробь 0,3(6) равна обыкновенной дроби, в числителе которой разность между всем числом после запятой - 36 и числом после запятой до периода 3, то есть 36-3=33, а знаменатель состоит из "девяток" и "нулей", причём "девяток" столько, сколько цифр в периоде -1,а "нулей" столько, сколько цифр после запятой до периода -1, то есть знаменатель будет равен - 90. ⇒
0,3(6)=33/90=11/30.
ответ: 0,3(6)=11/30.