Какое из уравнений имеет иррациональные корни? x^2+2x+1=0 x^2+2x-3=0 x^2+2x+2=0 x^2+2x-6=0

👇

Ответ:

TaHoC

17.04.2020

X^2 + 2x + 1 = (x + 1)^2 = 0
x^2 + 2x - 3 = (x + 3)(x - 1) = 0
x^2 + 2x + 2 = (x + 1)^2 + 1 = 0 - не имеет действительных корней.
x^2 + 2x - 6 = 0 - имеет иррациональные корни.

4,5(68 оценок)

Открыть все ответы

Ответ:

Сокол111111111

17.04.2020

ответ: 1) 5х-у=1

х+3у=5

у=-1+5х

х+3(-1+5х)=5

решаем уравнение: х+3(-1+5х)=5

х-3+15х=5 - 16х-3=5

16х=5+3=8 - х=8|16 - х=1|2

возвращаемся к системе: у=-1+5х получаем у=-1+5*1|2

х=1|2 у=3|2

2) 9х+2у=16

3х-5у=11

х=16|9-2|9у

3(16|9-2|9e)-5у=11

решаем уравнение: 3(16|9-2|9e)-5у=11 16|3-2|3y-5y=11

16|3-17|3y=11 |умножаем на 3 (чтобы убрать дробь)

16-17y=33

-17у=33-16 -17у=17 у=-1

возвращаемся к системе: х=16|9-2|9у получаем х=16|9-2|9*(-1)

х=16|9+2|9 х=2

х=2 у=-1

3) 2х-3(2у+1)=15

3(х+1)=3у=2у-2

убираем в первом уравнении скобки: 2х-6у-3=15 2х=15+6у+3 2х=18+6у (делим на 2) х=9+3у

получаем: х=9+3у

3(9+3у+1)+3у=2у-2

Решаем уравнение: 3(9+3у+1)+3у=2у-2

3(10+3у)+3у=2у-2

30+9у+3у=2у-2 30+12у=2у-2

12у-2у=-2-30 10у=-32 (делим обе стороны на 10) у=-16|5

возвращаемся к системе: х=9+3у получаем х=9+3*(-16|5) получаем х=-3|5 y=-16|5

если стоит этот знак | - то это дробь

4,6(90 оценок)

Ответ:

даун47

17.04.2020

Преобразуем левую часть:
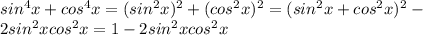
$sin^{4} x + cos^{4} x = ( sin^{2}x) ^{2} + (cos^{2}x) ^{2} = ( sin^{2}x + cos^{2}x) ^{2} - \\ 2 sin^{2} x cos^{2} x = 1 - 2 sin^{2} x cos^{2} x$

Далее:
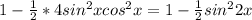
$1 - \frac{1}{2} * 4 sin^{2} x cos^{2}x = 1 - \frac{1}{2} sin^{2} 2x$
Таким образом, получаем уравнение:
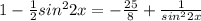
$1 - \frac{1}{2} sin^{2}2x = -\frac{25}{8} + \frac{1}{ sin^{2}2x }$
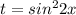Теперь понятно, что можно ввести замену $t = sin^{2}2x$ и продолжать решение уже дробно-рационального уравнения.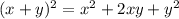

Советую запомнить приём, который я здесь употребил. Он состоит вот в чём.
Мы помним формулу сокращённого умножения:
$(x+y)^{2} = x^{2} + 2xy + y^{2}$
Отсюда я могу легко выразить сумму квадратов:
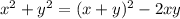
$x^{2} + y^{2} = (x+y)^{2} - 2xy$
Думаю, Вы уже догадались, что в нашем уравнении сыграло роль x, а что y.
Этот приём встречается очень часто в самых неожиданных ситуациях, так что рекомендую запомнить его.
Уравнение можно было решить и по формулам понижения степени(правда, это значительно было бы сложнее). Но в целом, можно рассмотреть и такой вариант, но я показал проще.

Делаем замену:
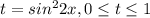
$t = sin^{2} 2x, 0 \leq t \leq 1$
После замены получаем:
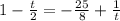
$1 - \frac{t}{2} = - \frac{25}{8} + \frac{1}{t}$
Умножаем обе части уравнения на 8t(с дробями работать крайне неудобно, да и t в знаменателе нам ни к чему - просто запомним, что он должен быть отличным от 0, а потом проверим это):
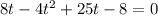
$8t - 4 t^{2} + 25t - 8 = 0$
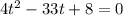
$4 t^{2} - 33t + 8 = 0$
Решаем квадратное уравнение(кстати, t уже отличен от 0. В этом можно убедиться прямой подстановкой)
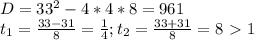$D = 33^{2} - 4 * 4 * 8 = 961 \\ 
 t_{1} = \frac{33 - 31}{8} = \frac{1}{4}; t_{2} = \frac{33 + 31}{8} = 8 \ \textgreater \ 1$ - этот корень не удовлетворяет нашему уравнению.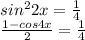
Следовательно, возвращаясь к переменной x, получаем простейшее уравнение:
$sin^{2} 2x = \frac{1}{4} \\ \frac{1 - cos 4x}{2} = \frac{1}{4}$
Отсюда
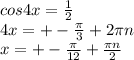
$cos 4x = \frac{1}{2} \\ 4x = +- \frac{ \pi }{3} + 2 \pi n \\ x = +- \frac{ \pi }{12} + \frac{ \pi n}{2}$
Это и есть ответ. Напомню, что при решении простейшего уравнения я использовал формулу понижения степени, а в конечном результате n - целое число.

4,7(25 оценок)

Это интересно:

Кулинария-и-гостеприимство

23.06.2020

Как заварить Кунг фу чай - лучший способ насладиться вкусом восточного чая...

Кулинария-и-гостеприимство

02.02.2020

Как сделать красивые и вкусные французские макароны с миндалем...

Здоровье

04.01.2023

Контроль гнева: как управлять своими эмоциями...

Семейная-жизнь