Нули функции – точки (точнее значения кординаты х) в которых график пересекает ось Ох, тоесть значения х при которых значение функции равно нулю.
1) у=15–2х
0=15–2х
2х=15
х=7,5
ответ: 7,5
2) у=2х²–98
2х²–98=0
Д=0²–4*2*(–98)=784
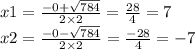
ответ: 7; –7
3) у=(4х–2)(х+1)
(4х–2)(х+1)=0
Совокупность:
4х–2=0
х+1=0
Совокупность:
4х=2
х=–1
Совокупность:
х=0,5
х=–1
ответ: 0,5; –1
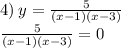
Система:
5=0
(х–1)(х–3)≠0
Так как 5≠0, то система корней не имеет, следовательно нулей у данной функции нет.
ответ: нет
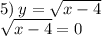
ОДЗ: х–4>=0
х>=4
х–4=0
х=4
4=4, значит значение подходит по ОДЗ.
ответ: 4
6) у=х²+4
х²+4=0
х²=–4
Квадрат числа не может быть отрицательным, значит корней нет.
ответ: нету
ответ: при х=1 и при х=-1
Объяснение:Точки пересечения графиков данных функций y=x²+4x+1 и y=kx можно найти, приравняв значения функций:
x²+4x+1 = kx
x²+4x+1 - kx =0
x²+(4-k)·x+1 = 0
По условию прямая y=kx и парабола y=x²+4x+1 имеют только одну общую точку, значит дискриминат полученного квадратного уравнения равен 0 (чтобы квадратное уравнение имело единственный корень), ⇒D=(4-k)² - 4·1·1= 16-8k+k²-4= k²-8k+12
k²-8k+12=0
k₁=2, k₂=6
Поэтому прямая у=2х и парабола y=x²+4x+1 имеют только одну общую точку⇒x²+4x+1 =2х⇒x²+2x+1 =0⇒ (х+1)²=0 ⇒ х=-1
прямая у=6х и парабола y=x²+4x+1 имеют только одну общую точку⇒x²+4x+1 =6х⇒ x²-2x+1 =0⇒ (х-1)² =0 ⇒ х=-1
х+3 км/ч - первоначальная скорость
120/(х+3)+54/х=3
120х+54(х+3)=3х(х+3)
120х+54х+162=3х²+9х
3х² - 165х-162=0
х² - 55х-54=0
D=55²+4*54=3241≈+-56,93²
х1=(55-56,93)/2= - 0,965 - не подходит решению
х2=(55+56,93)/2≈56
56+3=59(км/ч) - первоначальная скорость