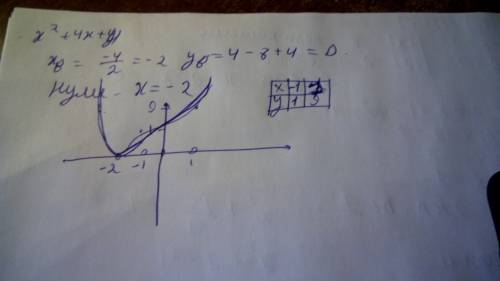
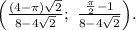
Объяснение:
Область 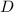 , задающая плоскую фигуру, координаты центра тяжести которого требуется найти, задана такими кривыми:
, задающая плоскую фигуру, координаты центра тяжести которого требуется найти, задана такими кривыми:
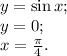
Известны ограничения сверху и снизу на 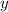 , а для
, а для  только сверху. Тогда ограничение снизу будет граничным с остальными:
только сверху. Тогда ограничение снизу будет граничным с остальными:
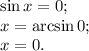
Получили четвёртое и последнее ограничение для области. Тогда область 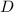 задана такими кривыми:
задана такими кривыми:
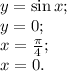
Переведём условия в вид неравенств:
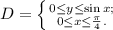
Поскольку левые части неравенств области нулевые, можем сразу вычислить площадь области, не используя двойной интеграл, а вместо него использовав одномерный определённый интеграл, в качестве функции использовав верхний предел 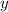 , а в качестве пределов интегрирования — части неравенства для
, а в качестве пределов интегрирования — части неравенства для  .
.
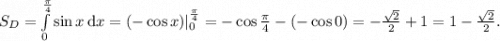
Как известно, если 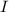 — точка центра тяжести, то
— точка центра тяжести, то 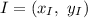 , и они в свою очередь:
, и они в свою очередь:
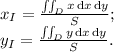
Найдём обе координаты точки центра тяжести.
Начнём с абсциссы:
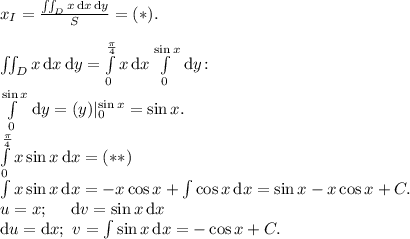
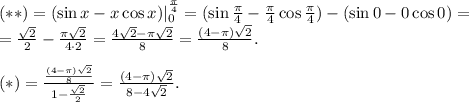
Теперь ордината:

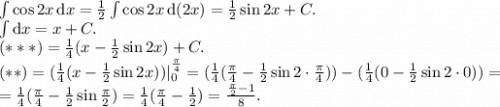
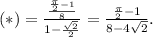
ответом будут найденные координаты, 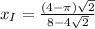 и
и 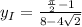 .
.