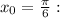Перейдем в исходном уравнении от корней к степеням с дробным показателем, тогда уравнение примет вид:
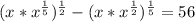
В получившемся уравнении перемножим степени в скобках как степени с одинаковым основанием, получим в результате равносильное уравнение:
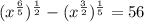
Отсюда по свойству степеней получим равносильное уравнение, применив свойство степень в степени:
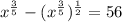
Сделаем замену в последнем уравнении: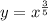 
Тогда последнее уравнении примет вид:
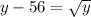-------(1)
Замечаем, что новая неизвестная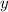 
должна удовлетворять условию:
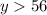--------(2) что следует из уравнения (1)
Возведем обе части уравнения в квадрат, после приведя подобные, получим квадратное уравнение:
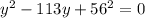
Для нахождения корней квадратного уравнения воспользуемся теоремой Виета:
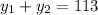
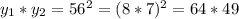
Отсюда получим искомые корни:
, 
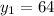При этом корень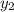 
посторонний, поскольку не удовлетворяет не равенству (2). Таким образом, исходное уравнение имеет один корень:
Вернем к старой неизвестной, получим:
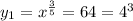, отсюда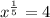 
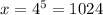
ответ: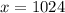 
1) lg11-lg110=lg11-lg(11*10)=lg11-(lg11+lg10)=lg11-lg11-lg10=-1
2) sin^4a-cos^4a+cos^2a
По формулам понижения степени:
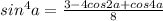
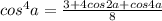
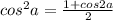
Подставляем и получаем:
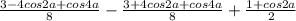
Приводим подобные и все под общий знаменатель и получаем:
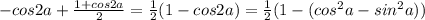
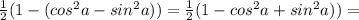
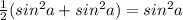
3)
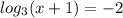
Найдем область определения:
х+1>0, т.е х>-1
Теперь решаем:
По определению логарифма получаем:
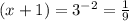
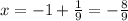
Решение лежит в области определения, значит оно удовлетворяет уравнению
4) Найти область определения функции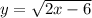 
Чтобы функция была определена на множестве действительных чисел R, необходимо чтобы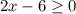 
что эквивалентно неравенству 
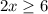, или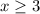 
Область определения функции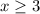
5) Найти период функции. По определению периода:
T-называется периодом функции F(x), если F(x+T)=F(x)
Подставим в нашу функцию:
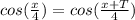
Нам известно, что период функции cos(x)=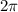
Т.е приходим к такому уравнению относительно Т:
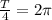, таким образом получаем что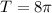 
6) Первообразная от функции является неопределенным интегралом, значит надо вычислить
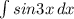
Сделаем простую замену u=3x, du=3dx отсюда dx=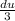
, в итоге получаем:
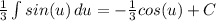
Вернемся к исходным переменным и получим:
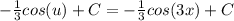, где C-константа.
ответ: Первообразная от функции y=sin(3x) будет равна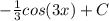 
Производная функции в точке