Сумма и разность считается след образом, например:
3_1/2 - 1_3/5 =
1) приводятся дроби к общему знаменателю;
=3_5/10 - 1_6/10 =
2) при вычитании, можно занимать целую часть в уменьшаемом для возможности работать с дробной частью
=2_15/10 - 1_6/10 =
3) вычитаем целые части, вычитаем дробные части, получаем
= 1_9/10
4) при необходимости и возможности производим сокращения в дробной части.
= 1_9/10 = 1,9 (в данном случаем перевели в десятичную дробь)
С суммой аналогично:
2_1/3 + 1_4/5 = 2_5/15 + 1_12/15 = 3_17/15 = 4_2/15
Умножение и деление смешанных чисел происходят след образом:
1_2/3 * 2_3/5 =
1) Переводим смешанные числа в неправильную дробь
= 5/3 * 13/5 =
2) числитель умножаем на числитель, знаменатель на знаменатель=
(5*13) / (3 * 5) =
3) производим сокращения, если они возможны
=13/ 3 =
4) выделяем целую часть в получившейся неправильной дроби:
=4_1/3
С делением аналогично, только действуем по правилам деления дробей, т е умножаем на дробь, обратную делителю.
2_3/4 : 1_5/6 = 11/4 : 11/6 = 11/ 4 * 6/11 = (11*6) / (4*11) = 6/4 = 3/2 = 1_1/2
Возьмем ваше же уравнение
lx+2l+lxl+lx-2l=4
Левую и правую части уравнения рассматриваем как функции.
f(x)=lx+2l+lxl+lx-2l и g(x)=4
С g(x) все понятно. Это прямая y=4, параллельна Ox.
С f(x) разбираемся. Это кусочная функция. Найдем нули подмодульных выражений:
x+2=0 ⇒ x=-2, x-2=0 ⇒ x=2, x=0.
Имеем интервалы (-∞; -2); [-2; 0); [0; 2); [2; +∞). Запишем равносильный переход:
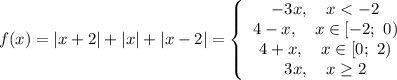
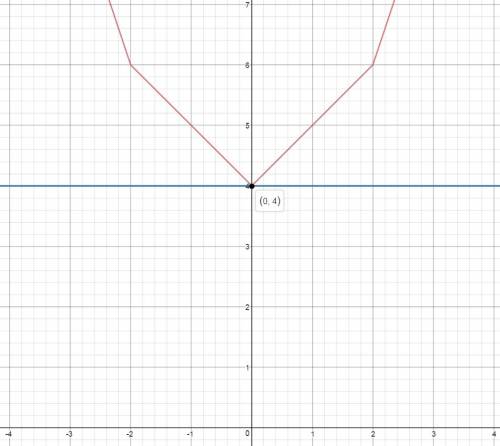
Построение графика на этом этапе элементарно. Из системы можно видеть, что функция f(x) четная. Достаточно построить или левую или правую ее часть, остальное отзеркалить. Готовый рисунок приложен.
х=-0,17-1,2
х=-1,37
2) 14-х=-28
х=14+28
х=42
3) х-9=3,1
х=9+3,1
х=12,1
4)-2,1-х=-2 I*(-1)
2,1+х=2
х=2-2,1
х=-0,1.