Сначала иследуем случай р=0 (коэффициент при x^2 равен 0)
получаем неравенство -2*(0-1)x+2*0<0; 2x<0; x<0 - значит при р=0 неравенство решения имеет
Далее пусть р не равно0, тогда неравенство - квадратное (а не линейное)
Чтобы оно не имело решений, необходимо и достаточно чтобы выполнялось два условия
1: p>0 (ветви параболы направлены верх)
2: D<0 (нет точек пересечения с осью абсцисс)
тогда график параболы будет лежать над осью Ох.
p>0
D=(-2(p-1))^2-4*p*2p=4p^2-8p+4-8p^2=-4p^2-8p+4<0
-4p^2-8p+4<0;
p^2+2p-1>0;
p^2+2p+1>2;
(p+1)^2>2
учитывая, то p>0 значит p+1>0 , то (случай p+1<-корень(2) - невозможен)
p+1>корень(2)
p>корень(2)-1
итого обьединяя получим ответ при р є 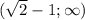
(3х - 2)(х - 3) = 20
3x² - 9x - 2x + 6 - 20 = 0
3x² - 11x - 14 = 0
D = (-11)² - 4 * 3 * (-14) = 121 + 168 = 289 = 17²
x1 = (11 + 17) / 6 = 28 / 6 = 14 / 3 = 4 целых 2/3
х2 = (11 - 17) / 6 = -1
ответ: 4 целых 2/3 или -1
(8х - 9)(3х + 2) - (2х - 3)(8х - 2) = 33х + 20
24х² + 16х - 27х -18 - 16x² + 4x + 24x - 6 - 33x - 20 = 0
8x² - 16x - 44 = 0 | : 4
2x² - 4x - 11 = 0
D = 16 + 88 = 104 = (2 √26)²
x1 = (4 + 2√26) / 4 = (2(2 + √26)) / 4 = (2 + √26) / 2
x2 = (4 - 2√26) / 4 = (2(2 - √26)) / 4 = (2 - √26) / 2
ответ : (2 + √26) / 2 или (2 - √26) / 2
40+40=80- еще одна
40+40=80- еще одна
80+80+80=240
За 240 рублей три шоколадки