1)Решение системы неравенств [-2, (-1+√73)/4]
2)Решение системы неравенств х∈(0,2, 1)
Объяснение:
1. Решите систему неравенств:
3х+4≤4х+6
х-5≤4-2х²
Во втором неравенстве перенесём все члены уравнения в левую часть, приравняем к нулю и решим, как квадратное уравнение:
х-5-4+2х²≤0
2х²+х-9=0
х₁,₂=(-1±√1+72)/4
х₁,₂=(-1±√73)/4
х₁=(-1-√73)/4 ≈ -9,5
х₂=(-1+√73)/4 ≈ 7,5
Начертим СХЕМУ параболы, которую обозначает данное уравнение (ничего вычислять не надо). Просто начертим схематично оси, параболу с ветвями вверх, и отметим на оси Ох точки х₁ ≈ -9,5 и
х₂ ≈ 7,5. Ясно видно, что у<0 при х от -9,5 до 7,5, то есть,
решение второго неравенства х∈[(-1-√73)/4, (-1+√73)/4]
Решим первое неравенство.
3х+4≤4х+6
3х-4х ≤6-4
-х ≤2
х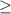
-2 знак меняется
Решение первого неравенства х∈[-2, ∞).
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств [-2, (-1+√73)/4] х от -2 до 7,5.
Неравенства нестрогие, скобки квадратные.
2. Решите двойное неравенство -3<2-5х<1
Решается как система:
2-5х>-3
2-5х<1
-5х> -3-2
-5x<1-2
-5x> -5
-5x< -1
x<1 знак меняется x ∈(-∞, 1) решение 1-го неравенства
x>0,2 знак меняется x ∈(0,2, ∞) решение 2-го неравенства
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств х∈(0,2, 1)
Неравенства строгие, скобки круглые.
Нельзя
Объяснение:
Немного общих вводных:
Функция — соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Ломаная линия – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Если концы ломаной совпадают, то такая ломаная называется замкнутой.
для простоты и наочности на примере рисунка из вложения :
пусть у нас есть замкнутая ламанаяА1А2А3А4А5
в нашем случае крайняя левая точка по оси Ох это А2, крайняя правая А5, путь от крайней левой до крайней правой точки можно осуществить двумя путями, в нашем случае либо (за часовой стрелкой) А2А1А5 либо (против часовой) А2А3А5
оба этих пути задают какието графики, но нельзя задать общим правилом функции ра на оба пути так как мы получим , что тогда между нашими крайними точками А2 и А5 для любого х будет как минимум по два значения , одно с "верхнего" пути ,второе с "нижнего", что противоречит определению функции.
Так что определение замкнутой ломаной входит в противоречие с определением для функции. Вывод - нельзя.
(замкнутая ломаная состоит минимум из трех вершин, и в ней в любом случае можно найти левую и правую крайнюю соотнося с осью координат, а вторая ось будет пересекать ломаную как минимум в двух точках между этими крайними)
ответ: x∈(-√7; 1]