-3К=-15
Объяснение:
Смотри, представим что наше - 3К это х, а 11 и - 4 обычные числа. Мы не можем складывать х и обычные числа, потому что у них нет коэффициента х. К примеру, мы могли бы сделать так: - 3К+2К и получилось бы 5К. Но смогли бы только потому, что после 2 есть коэффициент К. То есть, мы не сможем сделать так: - 3К+2, потому что у 2 нет К и мы не сможем решить уравнение дальше.
В нашем случае, так как мы не можем сложить 11 или - 4 с - 3К, потому что у них нет коэффициента К, то мы сложим их между собой.
-3К+11=-4
Так как мы не можем сложить что-либо с - 3К, то нам остаётся пронести 11 к - 4. Мы переносим это число за знак =. Но при переносе у нас ВСЕГДА знак меняется на противоположный.
Таким образом мы делаем так:
-3К=-4-11
Знак у - 4 мы оставляем так как мы переносим исключительно 11, а у него мы знак с + меняем на -.
И получается
-3К=-15
А - 11-4 будет - 15
Вот так и получается.
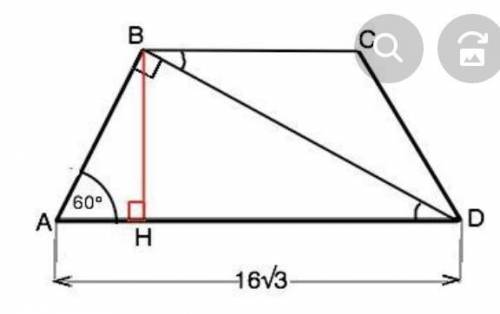
Обозначим трапецию АВСD, AB=CD, АD=16√3, ∠BAD=60°. ∠ABD=90°. Треугольник АВD- прямоугольный, ⇒ ∠АDB=180°-90°-60°=30°. Сторона АВ противолежит углу 30° и равна половине AD. АВ=8√3. Опустим высоту ВН на большее основание. Треугольник АВН - прямоугольный, ∠ АВН=180°-90°-60°=30°. Катет АН=АВ:2=4√3. ⇒ DH=AD-AH=16√3-4√3=12√3. Высота ВН=АВ•sin60°=8√3•(√3/2)=12. Высота равнобедренной трапеции, проведенная из тупого угла, дели основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности⇒ DH=(AD+BC):2. Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=BH•DH=12•12√3=144√3 (ед. площади)
==========
Как вариант решения можно доказать, что треугольник DCB - равнобедренный, ВС=CD=AB, вычислить длину высоты и затем площадь ABCD.